Fed2: Feature-Aligned Federated Learning
The notion of permutation invariance
- Given a Fully Connected Neural Net (FCNN) with two consecutive layers, one can swap the positions of two neurons in a layer and their associated weights entering and leaving the neurons without altering the outputs of the network. Formally, the FCNN \(F\) with weights \(w_0\) and \(w_1\) given input X is invariant to any permutation matrix:
- The same happens to Convolutional Networks and their filters.
- It implies a complex problem in Model Fusion and Federated Learning: How to be sure that the neurons combined by averaging parameters encode the same learned features ?.
- Previous methods used neurons matching based on the distance between weight matrices or activation values [1], computation of a Wasserstein barycenter [2] or Bayesian probabiltistic models [3].
Highlights
- The authors propose a new way of dealing with such a problem: align the learned features during local training instead of matching neurons after training local models.
- They define a neural structure with groups of parameters dedicated to groups of classes,
- Groups of parameters dedicated to the same classes are averaged together during the aggregation step of Federated Averaging.
- They show that they outperform matched aggregation methods in terms of computational cost, communication cost and final accuracy.
Methods
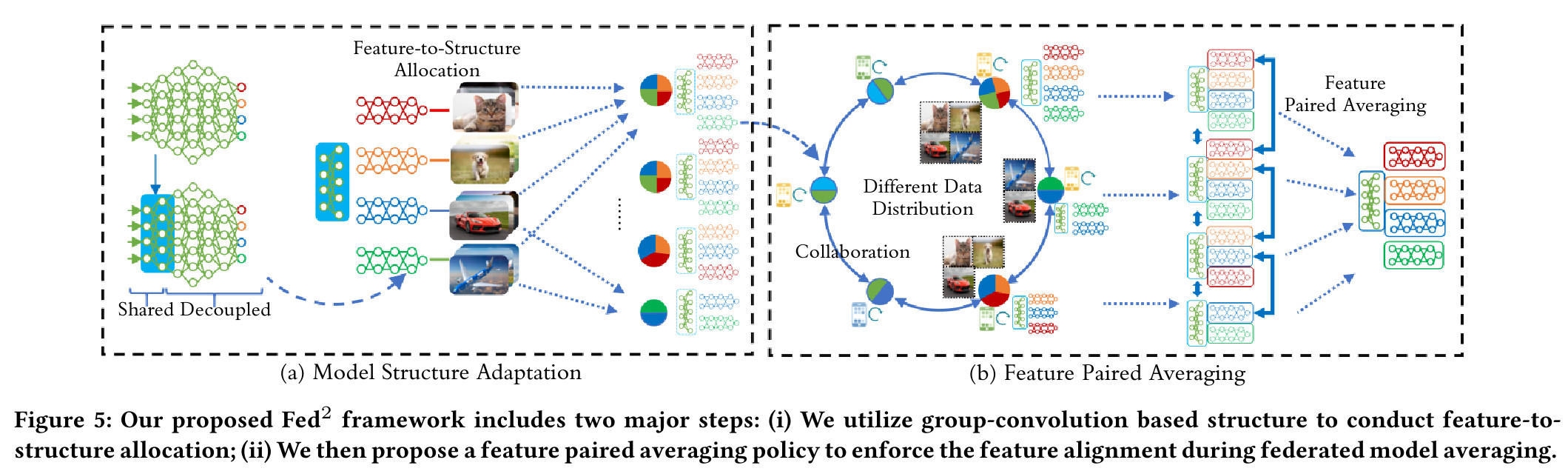
They define before training which parts of the local networks will be aggregated together, by fixing which class logits are outputted by which groups of parameters in the model architecture.
Feature allocation strategy
- After a number of classical convolutional layers, use group convolution to partition the network into independent parts,
- Do not use fully connected layer at the end, but one connected head on each group, outputting the logits of specific classes (partitioned among groups),
- Leverage the evolution of the total variation of features of a layer to determine at which depth to decouple the parameters (e.g. how many layers are kept shared).

Results
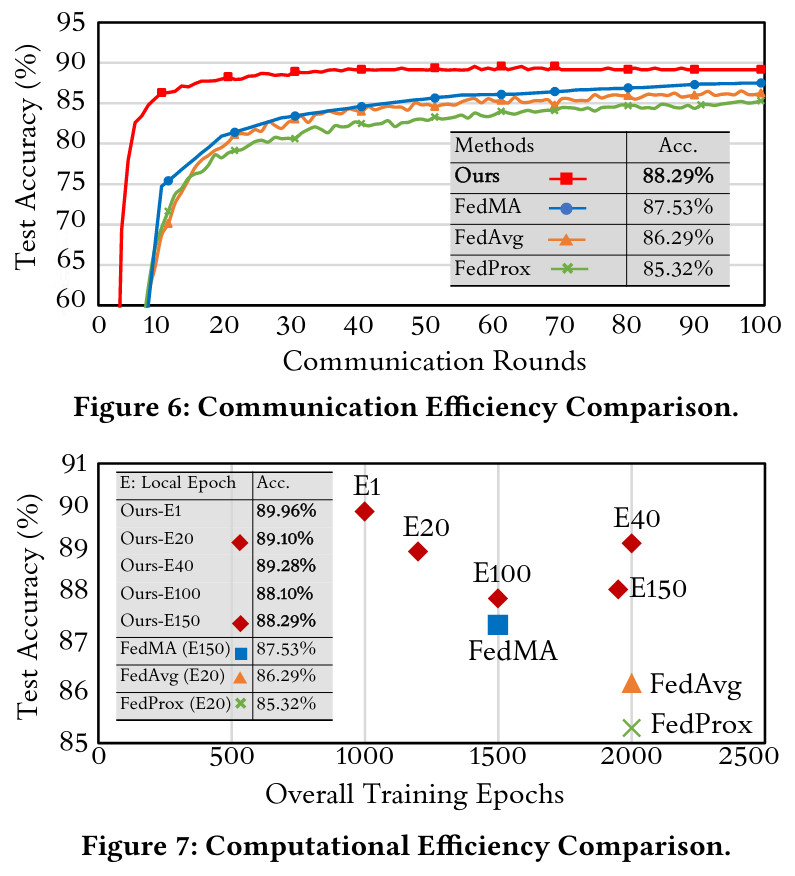
They show in tables below that their method outperforms Federated Averaging and a classical Matched averaging method on CIFAR10 in terms of final accuracy, communication cost and computation cost.
They show similar results on CIFAR100, to highlight the fact that the decoupling strategy works even with a high number of classes.
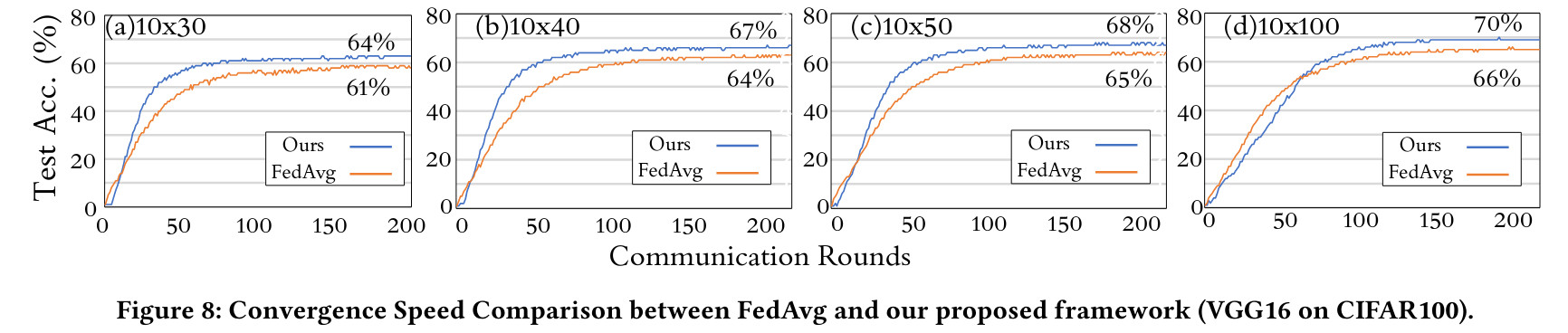
However, they also show that a smaller number of groups of parameters can improve final performance (decoupling parameters until having one head for each class is not optimal).

Conclusions
Solving the problem of feature matching to compute meaningful average of different models might be done by conditionning the location of learned features before training.