Context

  • Ultrafast imaging requires less acquisitions than conventional ultrasound focused imaging. However, it needs the compounding of several acquisitions to compensate for the lower image contrast and resolution. Therefore, there is a trade-off between image quality and image rate.
  • In a previous work, the same authors developed ID-Net (Inception for Diverging-wave Network), a CNN for the compounding of 3 RF acquisitions and reached the same quality than when using 31 RF acquisitions [1].
  • The objective of this paper is to develop a CNN that takes IQ signals as an input instead of RF signals, to reduce data size and power requirement. The main difficulty is that, unlike RF signals, IQ signals are complex.
  • The authors develop CID-Net (Complex-valued Inception for Diverging-wave Network), a complex CNN.

Highlights

  • Implementation of a complex convolution inspired by the multiplication of complex numbers.
  • Definition of a complex activation function based on the complex module.
  • Experimental demonstration that CID-Net reaches the same performance than ID-Net and outperforms the straightforward method of processing the real and imaginary parts separately (2BID-Net, 2-Branch Inception for Diverging-wave Network).

Methods

The complex CNN has 3 main building blocks:

  • The complex convolution was defined in [2] and uses complex weights \(W = W_r + jW_i.\) It is defined as:
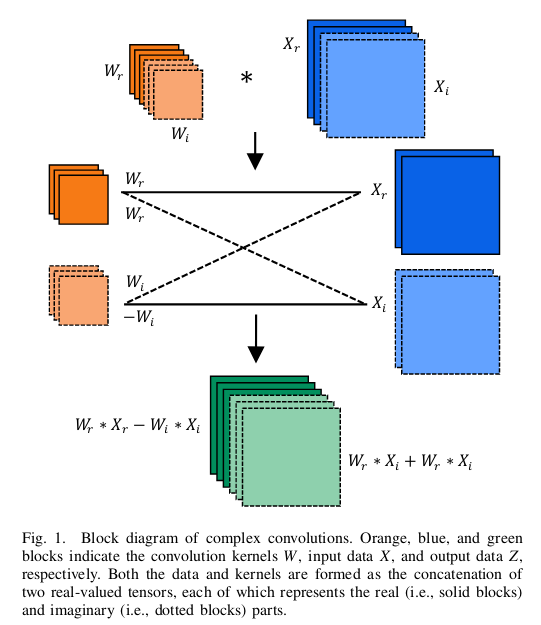
\[Z \left[\begin{array}{c} \operatorname{Re}(W * X) \\ \operatorname{Im}(W * X) \end{array}\right]=\left[\begin{array}{cc} W_{r} & -W_{i} \\ W_{i} & W_{r} \end{array}\right] *\left[\begin{array}{c} X_{r} \\ X_{i} \end{array}\right]\]

Obs: In the figure above, the bottom right expression should be: \(W_{i} * X_{r} + W_{r} * X_{i}.\)

  • The maxout activation function (MU) used in the previous work is replaced by the amplitude maxout (AMU). Given a complex convolutional layer output \(Z\) and its module \(Z_a = \lvert Z\rvert\), the amplitude maxout of \(Z\) is defined as:
\[\left[\begin{array}{c} \operatorname{Re}(\text{AMU}(Z)) \\ \operatorname{Im}(\text{AMU}(Z)) \end{array}\right]=\left[\begin{array}{cc} \operatorname{Re}(Z)\left[\operatorname{argmax}\left(Z_{a}\right)\right] \\ \operatorname{Im}(Z)\left[\operatorname{argmax}\left(Z_{a}\right)\right] \end{array}\right]\]

This activation allows to maintain both phase and module information as data is not modified.

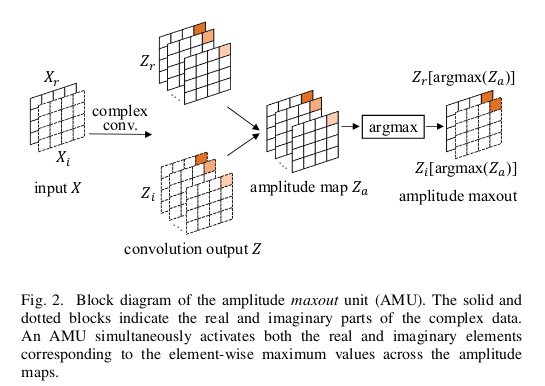
  1. The loss function is the complex mean squared error.
\[L(\Theta)=\frac{1}{n} \sum_{i=1}^{n}\left\|\hat{Y}_{i}-Y_{i}\right\|^{2}\]

Back-propagation is performed with respect to the real and imaginary parts of the weights.

“In order to perform backpropagation in a complex-valued neural network, a sufficient condition is to have a cost function and activations that are differentiable with respect to the real and imaginary parts of each complex parameter in the network.” [2]

Obs: Both ID-Net and CID-Net include an inception layer that applies kernels of different sizes in a given layer, thus generating feature maps with different receptive fields. The authors observed better results when using an inception layer, as it compensates for the signal sectorial shape [1].

Results

  • CID-Net with 3 acquisitions reaches the image quality of ID-Net and outperforms 2BID-Net and conventional compounding with 31 acquisitions.

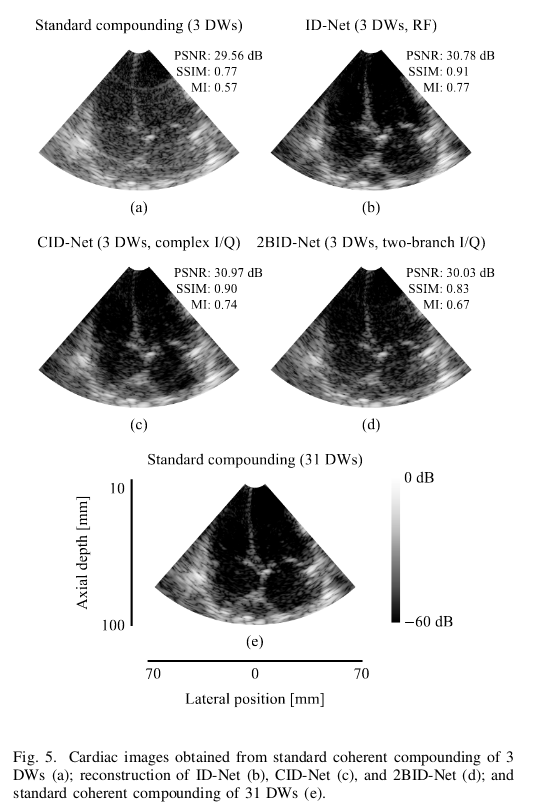
  • CID-Net outperforms 2BID-Net and conventional compounding in terms of contrast.

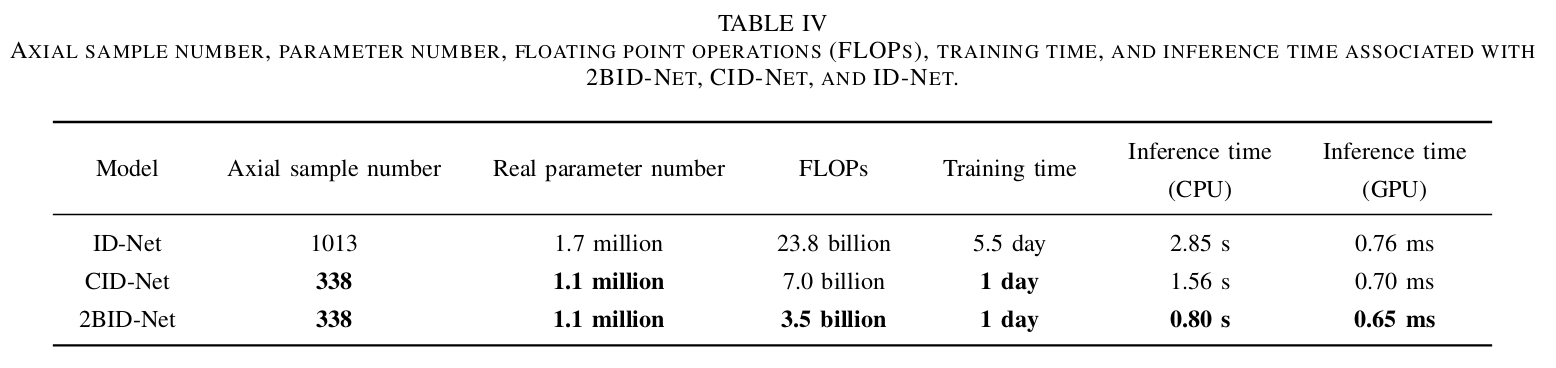
  • Data size and power consumption are greatly reduced by using IQ signals.

Conclusions

The authors develop complex CNN to process IQ signals for ultrafast image reconstruction with 3 acquisitions. They reach the same reconstruction quality than with the analogous problem that processes RF signals. The reconstruction quality is worse when they use a 2-branch CNN that does not account for the signal complex structure. Working with IQ signals leads to less computation time and data volume than RF signals.