What Do We Mean by Generalization in Federated Learning?
Introduction
The authors propose to reformulate the expected risk minimization problem commonly considered in machine learning optimization as a two level minimization problem in a federated setup, defining the risk on a distribution of local distributions. From there, they try to explore the notions of generalization and overfitting in a federated context.
Highlights
- Define the participation gap, reveal its connection with data heterogeneity, and explain differences in generalization behavior between label-based partitioning and semantic partitioning.
- Propose a three-way split for measuring out-of-sample and participation gaps in centralized and FL settings where data is drawn from a distribution of distributions,
- Observe significant participation gaps across different tasks and perform empirical studies on how number of clients, client diversity, etc. affect generalization performance,
- Observe significant differences in generalization behavior across naturally-partitioned and synthetically-partitioned federated datasets,
- Propose semantic partitioning as a synthetic partitioning principle.
Theoretical contributions
Definition of a federated learning problem
To correctly present the few theoretical ideas of the paper, we rewrite the notations and hypothesis of the authors.
- Let \(\Xi\) be the collection of all the possible image-label pairs,
- For any parameters \(w\) in a parameter space \(\Theta\), \(f(w,\xi)\) the loss at element \(\xi\in\Xi\) with parameter \(w\),
- Let \(C\) be the collection of all the possible clients. A client \(c\in C\) is associated with a local distribution \(D_c\) supported on \(\Xi\),
- Assume there is a meta-distribution \(P\) supported on client set \(C\), and each client \(c\) is associated with a weight \(\rho_c\) for aggregation.
The proposed formulation of a federated learning problem in this setup is to optimize
\[F(w) = F_{unpart}(w) := \mathbb{E}_{c\sim P}\left[\rho_c*\mathbb{E}_{\xi\sim D_c}[f(w,\xi)]\right]\]The formulation is more justified in a cross-device setting (with a large amount of clients, e.g. local distributions).
Empirical risks and generalization gaps
- Let \(\hat{C}\) be the participating clients, drawn from the meta-distribution \(P\),
- For each \(c\in\hat{C}\), let \(\hat{\Xi}_c\) be the participating training client data, drawn from the local distribution \(D_c\).
They further define the empirical risk on the participating training client data with
\[F_{part\_train}(w) := \frac{1}{|\hat{C}|}\underset{c\in \hat{C}}{\sum}[\rho_c*(\frac{1}{|\hat{\Xi}_c|}\underset{\xi\in\hat{\Xi}_c}{\sum} f(w,\xi))]\]And the semi-empirical risk on the participating validation client data with
\[F_{part\_val}(w) := \frac{1}{|\hat{C}|}\underset{c\in\hat{C}}{\sum}[\rho_c*(\mathbb{E}_{\xi\sim D_c}f(w,\xi))]\]They finally define two levels of generalization gap:
- The out-of-sample gap: \(F_{part\_val}(w) - F_{part\_train}(w)\)
- The partipation gap: \(F_{unpart}(w) - F_{part\_val}(w)\)
Highlighted properties
The participation gap:
- is an intrinsic property of FL due to heterogeneity. The gap will not exist if data is homogeneous,
- can quantify client diversity (comparable between tasks),
- can measure overfitting on the population distribution,
- can quantify model robustness to unseen clients,
- can quantify the incentive for clients to participate.
Practical contributions
The three-way validation split
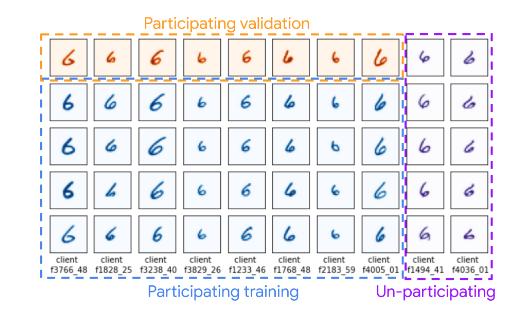
Each column corresponds to the dataset of one client. A dataset is split into participating training, participating validation, and unparticipating data, which enables separate measurement of out-of-sample and participation gaps.
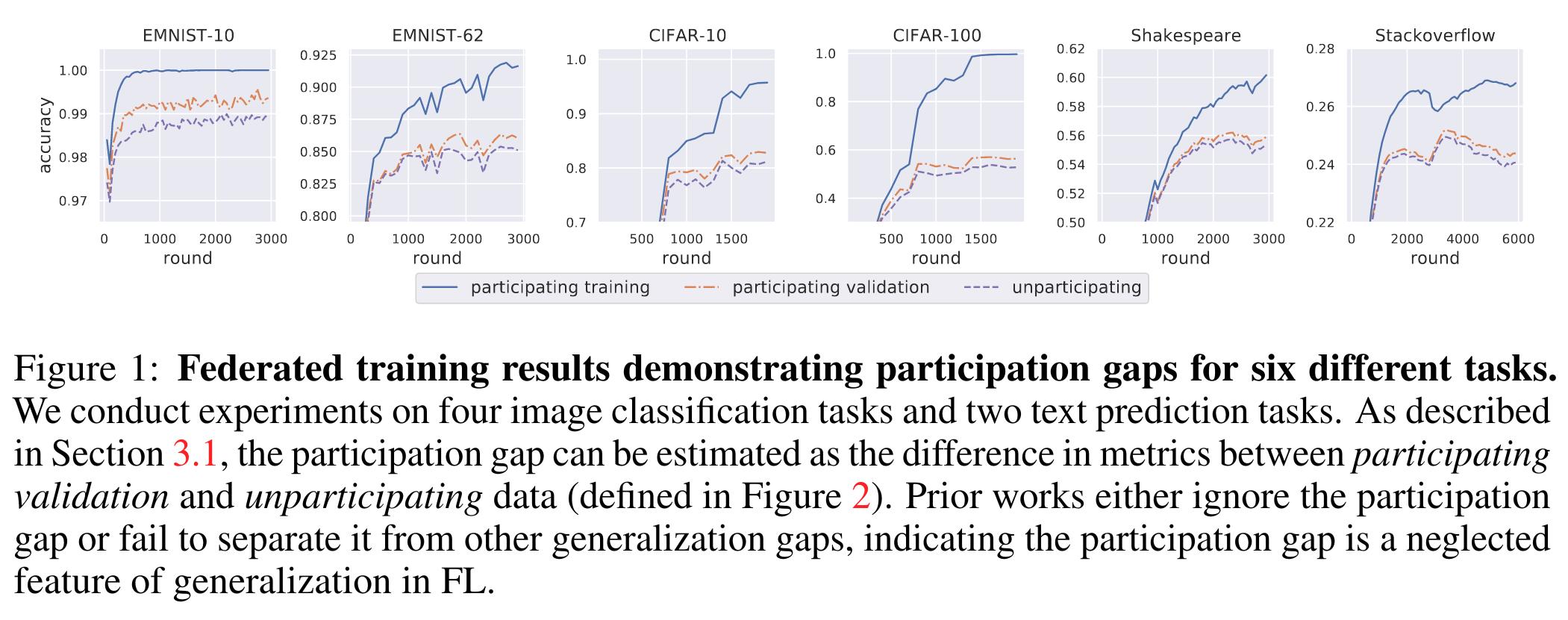
Two levels of generalization gap in practice
- With federated learning
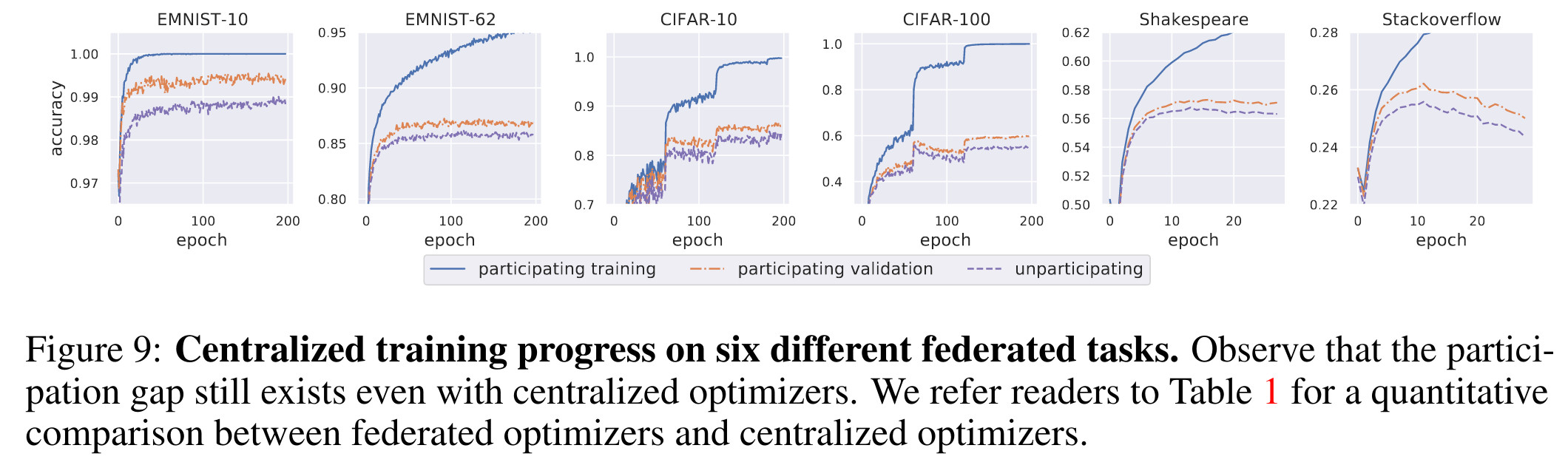
- But even with centralized training
Label partitioning is not enough to simulate heterogeneity
- To explore federated learning when there are no large federated datasets accessible, one can synthetically partition a public dataset.
- Simulating the heterogeneity of a federated dataset by generating partitions with different label distributions alter the training processes compared to a naturally heterogeneous federated dataset.

Semantic partitioning
The proposed partitioning protocol is the following for a classification task:
- For each label, extract semantic features with a pretrained neural network. Fit a Gaussian Mixture Model to cluster pretrained embeddings into \(C\) groups: intra-client intra-label consistency.
- Then, the aim is to compute an optimal multipartite matching with cost-matrix defined by KL-divergence between the Gaussian clusters. They approximate an optimal solution by sequentially solving the optimal bipartite matching for randomly-chosen label pairs: intra-client inter-label consistency.

Conclusions
- The authors proposed variants of the classical empirical risk adapted to heterogeneous federated learning,
- They proposed a three-way validation split to measure the two highlighted generalization gaps,
- They proposed a semantic partitioning to synthetize realistic heterogeneous partitionings of classification datasets.