FedAMP: Personalized Cross-Silo Federated Learning on Non-IID Data
Highlights
- The authors propose a new federated personalization method,
- The goal is to facilitate pairwise collaborations between institutions with similar data,
- The method is based on an alternation between optimization of local losses and of a message passing regularizer,
- The method can be applied to any supervised learning task (classification, segmentation, etc.).
Method
Problem definition
Consider a federated learning problem with \(M\) institutions, each with \(n_m\) samples.
Given \(W:= [w_i]_{i<M}\) the matrix of personalized model’s parameters \(w_i\in\mathbb{R}^d\), let’s define the overall personalized objective function:
\[\mathcal{F}(W) := \sum_{i=1}^MF_i(w_i)\]and the message passing regularizer:
\[\mathcal{A}(W):= \sum_{i<j}^MA(||w_i-w_j||^2)\]The function \(A:[0, \infty) \rightarrow \mathbb{R}\), with \(A(0)=0\), is increasing, concave, continuously differentiable and \(lim_{t\rightarrow 0^+}A'(t)\) is finite (they use \(A(||w_i-w_j||^2) = 1 - e^{-||w_i-w_j||^2/\sigma}\)). It measures the difference between \(w_i\) and \(w_j\) in a non-linear manner. Given the defintions above, the proposed optimization problem becomes:
\[\underset{W}{min\ }\{\mathcal{G}(W) := \mathcal{F}(W) + \lambda\mathcal{A}(W)\}\]Algorithm
The authors propose Federated Attentive Message Passing (FedAMP), an optimization scheme alternating between optimization of \(\mathcal{A}(W)\) and \(\mathcal{F}(W)\). Following their algorithm, at each global iteration \(k\):
-
Apply a gradient step on \(\mathcal{A}(W^k)\) to compute the cloud models:
\[U^k = W^k - \alpha_k\nabla\mathcal{A}(W^{k-1})\] -
Apply a proximal point step to optimize \(\mathcal{F}(W)\), e.g. train personalized models \(w_i, i\leq M\) for some epochs regularized by \(U^k\):
\[W^k = \underset{W}{arg min\ }\mathcal{F}(W) + \frac{\lambda}{2\alpha_k}||W-U^k||^2\]

- The authors provide convergence guarantees in cases where both \(\mathcal{F}\) and \(\mathcal{A}\) are convex, and when they are only continuously differentiable with Lipschitz continuous gradients.
Interpretation
-
The authors show that the proposed scheme induces that the cloud models \(u_i^k\) for each institution \(i\leq M\) at global iteration \(k\) is a convex combination of personalized models \(w_i^k\) through
\[\begin{split}u^k_i & = (1 - \alpha_k\sum_{i\neq j}^MA'(||w_i^{k-1} - w_j^{k-1}||^2))*w_i^{k-1} + \alpha_k\sum_{i\neq j}^MA'(||w_i^{k-1}-w_j^{k-1}||^2)*w_j^{k-1} \\& = \sum_{j=1}^M\xi_{i,j}w_j^{k-1}\end{split}\]with \(\forall i\leq M, \sum_{j=1}^M\xi_{i,j} = 1\)
-
Regularizing local training with such \(u_i^k\) can be viewed as a form of message passing between institutions. The closer two personalized models from different institutions are, the larger their contribution to each other is.
Heuristic improvement for deep neural networks
- Using Euclidean distance between personalized models can be ineffective when dealing with neural networks with a large number of parameters \(d\).
- The authors propose to use the following convex combinations of models for the cloud models instead, with \(\xi_{i,i}\) a self-attention hyper-parameter
Experiments
- Synthetically partitioned classical datasets are leveraged (MNIST, FashionMNIST, ExtendedMNIST, CIFAR100).
- The authors propose three types of partitioning:
- IID partitioning,
- A “pathological” partitioning with two classes per institution,
- A “practical” partitioning with groups of institutions owning the same data distribution, each containing a set of dominant classes different from other groups.
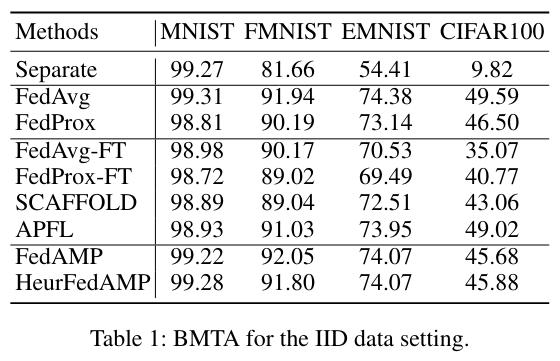
They show that personalization is obviously useless in cases where there is no domain shift between institutions.
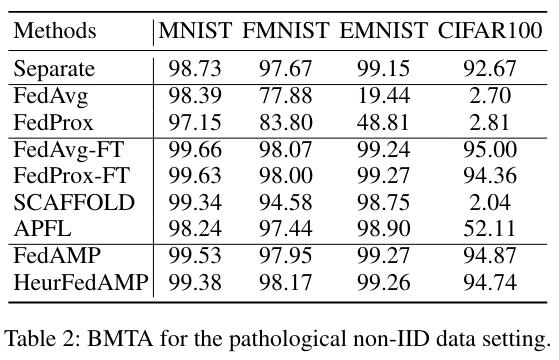
The pathological case breaks FedAvg and FedProx, while personalization techniques enable to recover parts of the performance.
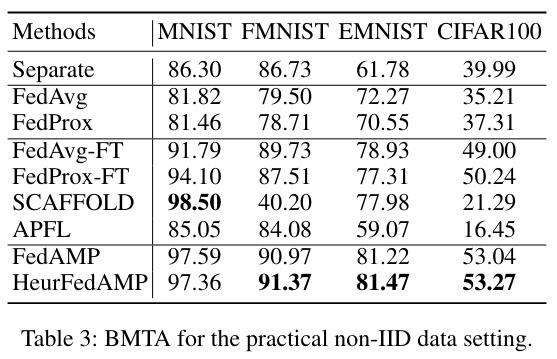
The practical case is a more realistic case, showing the potential of FedAMP as a personalization scheme.

In the practical case, the authors show that their optimization framework enables to recover the groups of institution through the matrix of \(\xi_{i,j}\), correctly clustering institutions together during learning.
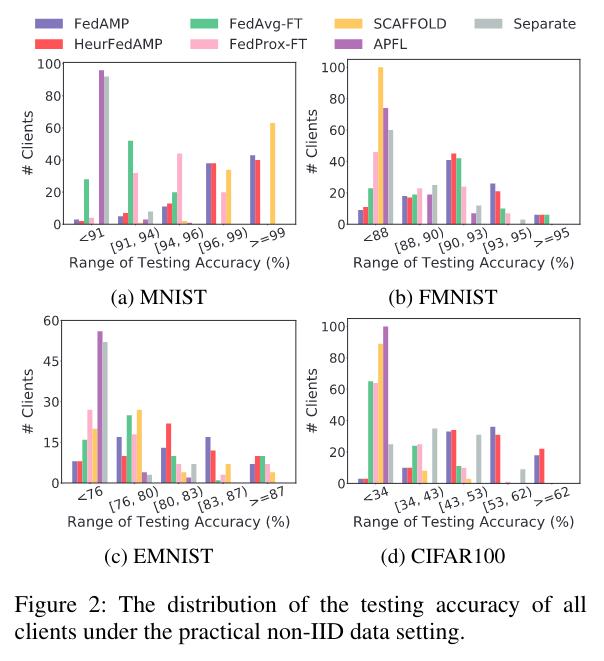
They quickly explore the fairness brought by FedAMP, significantly improving median performance across institutions (Wilcoxon signed-rank test).
Conclusions
- The authors proposed a novel federated personalization framework, based on message passing regularization,
- They provided convergence guarantees for their algorithm,
- They experimented on three interesting synthetic partitionings, highlighting in which case personalization can be beneficial.