Multi-Channel Stochastic Variational Inference for the Joint Analysis of Heterogeneous Biomedical Data in Alzheimer's Disease
Notes
- Unsupervised method.
- Gaussian linear case (for validation purposes)
- Another paper based on deep learning methods was done in 2019 by the same authors: Sparse Multi-Channel Variational Autoencoder.
-
A Github repository is available for the 2019 paper.
- Link to the VAE tutorial
Highlights
- The aim of this paper is to take into account several types of inputs (which are referred to as channels in the paper) for a better joint analysis.
- They proposed a novel multi-channel stochastic generative model.
- Their proposed method can have applications for generic data fusion techniques.
Introduction
When a patient suffers from Alzheimer’s disease, physicians use lots of sources of information. However, simple univariate correlation analysis are limited in modeling power. To overcome the limitations of mass-univariate analysis, methods such as PLS, RRR, CCA, and their variants (non-linearity, multi-channels) were used in biomedical research. The main issue is that those methods are not generative. The authors proposed a novel multi-channel stochastic generative model for the joint analysis of multi-channel heterogeneous data.
Methods
Let \(\textbf{x} = \{\textbf{x}_c\}_{c=1}^{C}\) be a single observation of a set of C channels, where each \(\textbf{x}_c \in \mathbb{R}^{d_c}\) is a \(d_c\)-dimensional vector.
- \(p(\textbf{z})\) : prior
- \(p(\textbf{x}_c \vert \textbf{z}, \pmb{\theta}_c)\) : likelihood distribution
- \(q(\textbf{z} \vert \textbf{x}_c, \pmb{\phi}_c)\) : probability density function
The objective can be formulated as:
\[\underset{q \in Q}{\operatorname{arg min}} \: \mathbb{E}_c[D_{KL} (q (\textbf{z} \vert \textbf{x}_c, \pmb{\phi}_c) \parallel p (\textbf{z} \vert \textbf{x}_1, \dots , \textbf{x}_C , \pmb{\theta}) )]\]By rearranging the objective, the authors obtain a lower-bound:
\[\mathbb{E}_c \left[ \mathbb{E}_{q(\textbf{z} \vert \textbf{x}_c )} \left[ ln \: p(\textbf{x} \vert \textbf{z}, \pmb{\theta}_c) \right] − D_{KL} (q (\textbf{z} \vert \textbf{x}_c, \pmb{\phi}_c) \parallel p (\textbf{z}) ) \right]\]A few interesting points to note about this new formulation are:
- The data matching term naturally emerges from reformulating the posterior constraint, independently from the data matching term commonly imposed by autoencoders;
- The inner expectation enforces the decoders from each channel to accurately reconstruct their respective channels.
Finally, under the hypothesis that channels are conditionally independent from each other given \(\textbf{z}\), the authors factorize the data likelihood as \(p(\textbf{x} \vert \textbf{z}, \pmb{\theta}_c) = \sum_{i=1}^{C} p(\textbf{x}_i \vert \textbf{z}, \pmb{\theta}_c)\) to reformulate the lower bound like below:
\[\mathscr{L}(\pmb{\theta}, \pmb{\phi}, \textbf{x}) = \mathbb{E}_c \left[ \mathbb{E}_{q(\textbf{z} \vert \textbf{x}_c )} \left[ \sum_{i=1}^{C} ln \: p(\textbf{x}_i \vert \textbf{z}, \pmb{\theta}_c) \right] − D_{KL} (q (\textbf{z} \vert \textbf{x}_c, \pmb{\phi}_c) \parallel p (\textbf{z}) ) \right]\]This factorization of the data likelihood enforces that the posterior from each channel should be similar, since they are used to reconstruct the input from other channels.
A figure from the Github repository explains schematically the general idea:
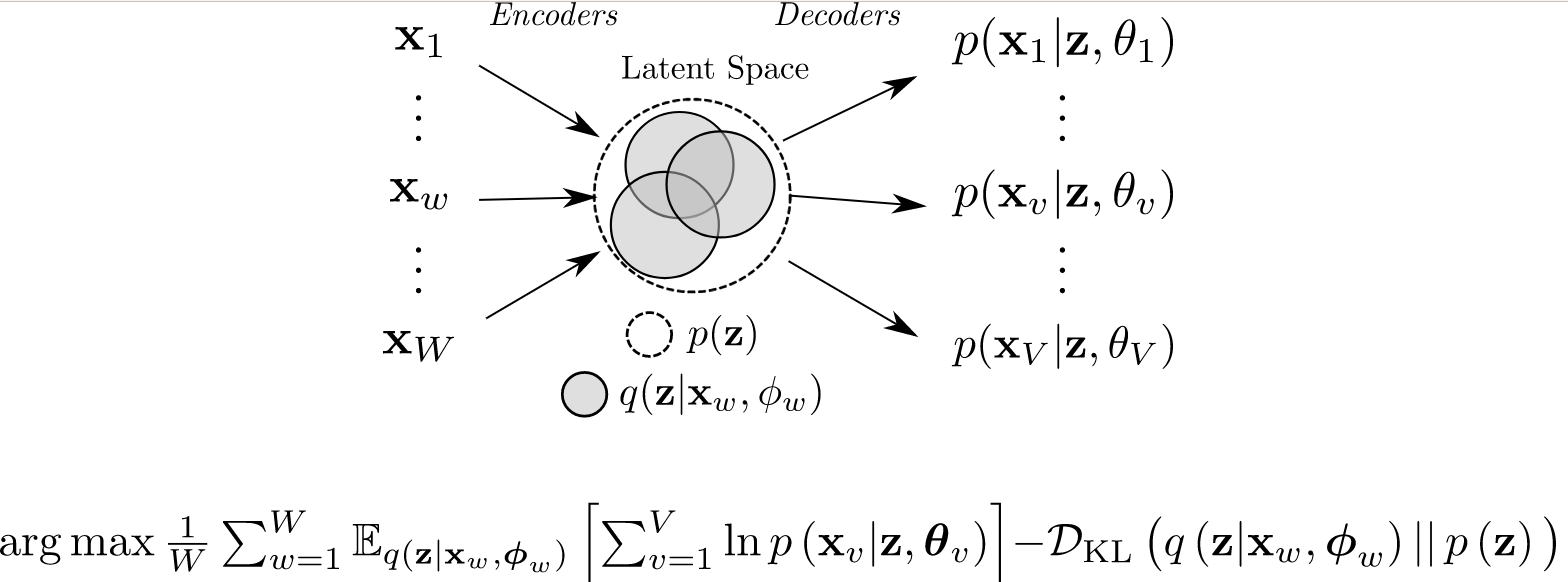
Results
- They created synthetic data (according to the equations shown below) and tested them with different parameters to prove the viability of their model.
- Here are the results with synthetic data :
 It shows that their model performs well compared to a single-channel model.
It shows that their model performs well compared to a single-channel model.
- They tried it on real data as well:
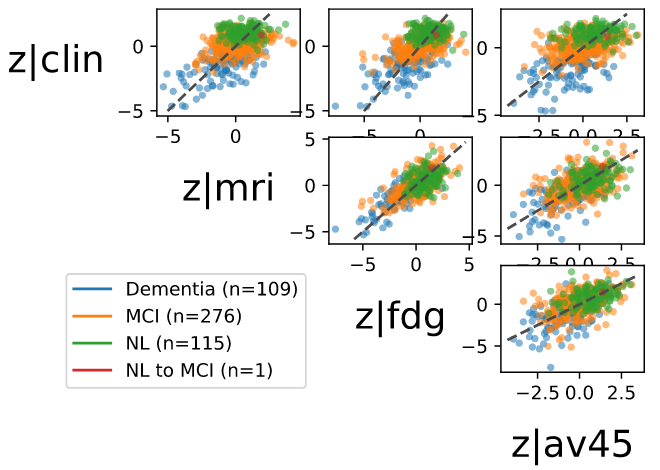
Fig. 3: Pairwise representations of one latent dimension (out of 16) inferred from each of the four data channels. Although the optimization is not supervised to enforce clustering, subjects appear stratified by disease classes.
- An example of generated data :
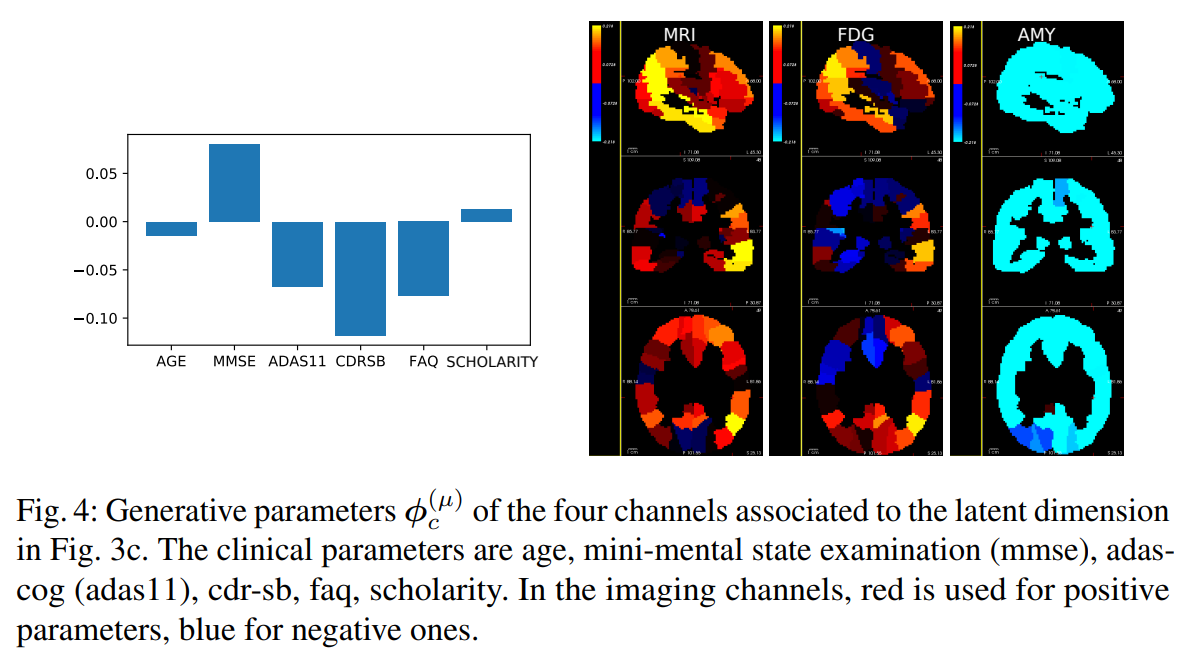 Having a generative model allows them to validate the latent space they obtained.
Moreover, the results they obtain are coherent with typical results from the literature on Alzheimer’s Disease.
Having a generative model allows them to validate the latent space they obtained.
Moreover, the results they obtain are coherent with typical results from the literature on Alzheimer’s Disease.
Conclusion
- Multi-channel model that jointly analyzes multi-modality data.
- Model that can generate data from the latent space
- Linear method (that can be easily changed with deep learning methods)