Highlights

  • New transformer architecture to perform audio-visual fusion, called Multimodal Bottleneck Transformer (MBT), which forces exchange of information between modalities to pass through specially designated latent tokens;
  • Limiting cross-attention between modalities as the additional benefit of avoiding the quadratic scaling cost of full pairwise attention;
  • To the best of my knowledge, the paper provides the first ablation study regarding design decisions for fusion (e.g. early vs late, etc.) in the context of transformers.

Introduction

Historically, methods to perform fusion focused mostly on either late fusion (where inputs are processed separately and the outputs are then merged together in some way, e.g. averaging logits of two modality-specific networks) or early fusion (where the inputs are minimally processed to that they can be fed to one model, i.e. tokenizing audio/video and concatenating the tokens from both modalities as input to a single transformer model).

With the advent of deep learning, more sophisticated fusion strategies were proposed, such as projection to joint (intermediate) latent spaces. The recent transformer architecture 1 2 then came along, which assumes very little about the structure of its inputs and can thus be used with minimal tweaking on vastly different types of data. Because of this, transformers seem like a prime candidate for a general multimodal architecture.

However, precisely because of their capacity to handle different types of data, multimodal applications of transformers have mostly “regressed” to simple early/late fusion approaches. In this context, one of the novelties of this paper is its study of different fusion paradigms using transformers.

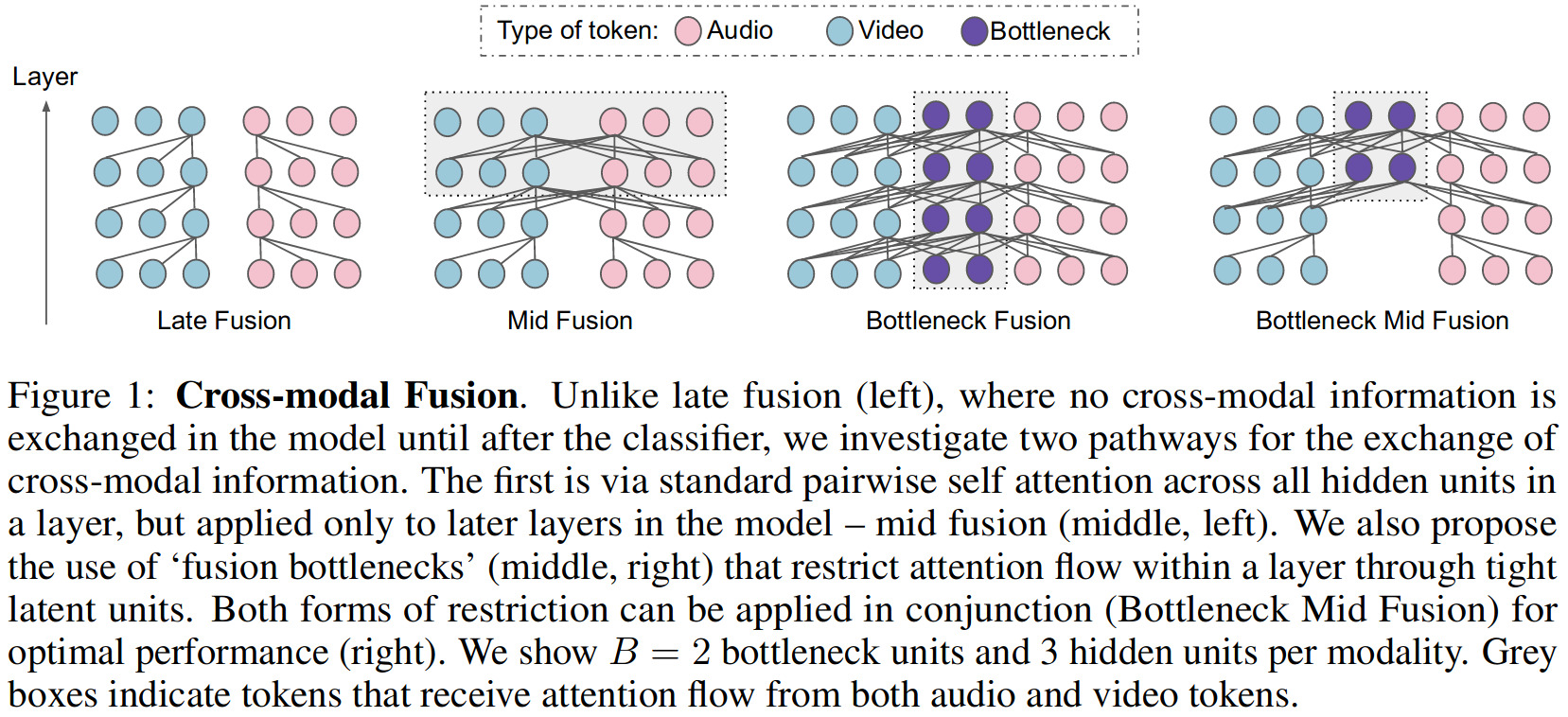
Methods

The main idea of the paper is to restrict the flow of cross-modal information between latent tokens by only performing cross-attention between each modality’s tokens, \(\mathbf{z}_i\), and a shared set of predefined fusion tokens \(\mathbf{z}_{\text{fsn}}\). Because there is much fewer of these fusion tokens then there are tokens assigned to each modality (\(N_{\text{fsn}} \ll N_{i}\)), the fusion tokens end up acting as a bottleneck to the flow of information between modalities. The authors argue that this is beneficial because i) it allows layers to specialize in learning unimodal patterns, and ii) it forces the model to “condense” information from each modality, eliminating redundancy which is common in high-dimensional data like images/videos.

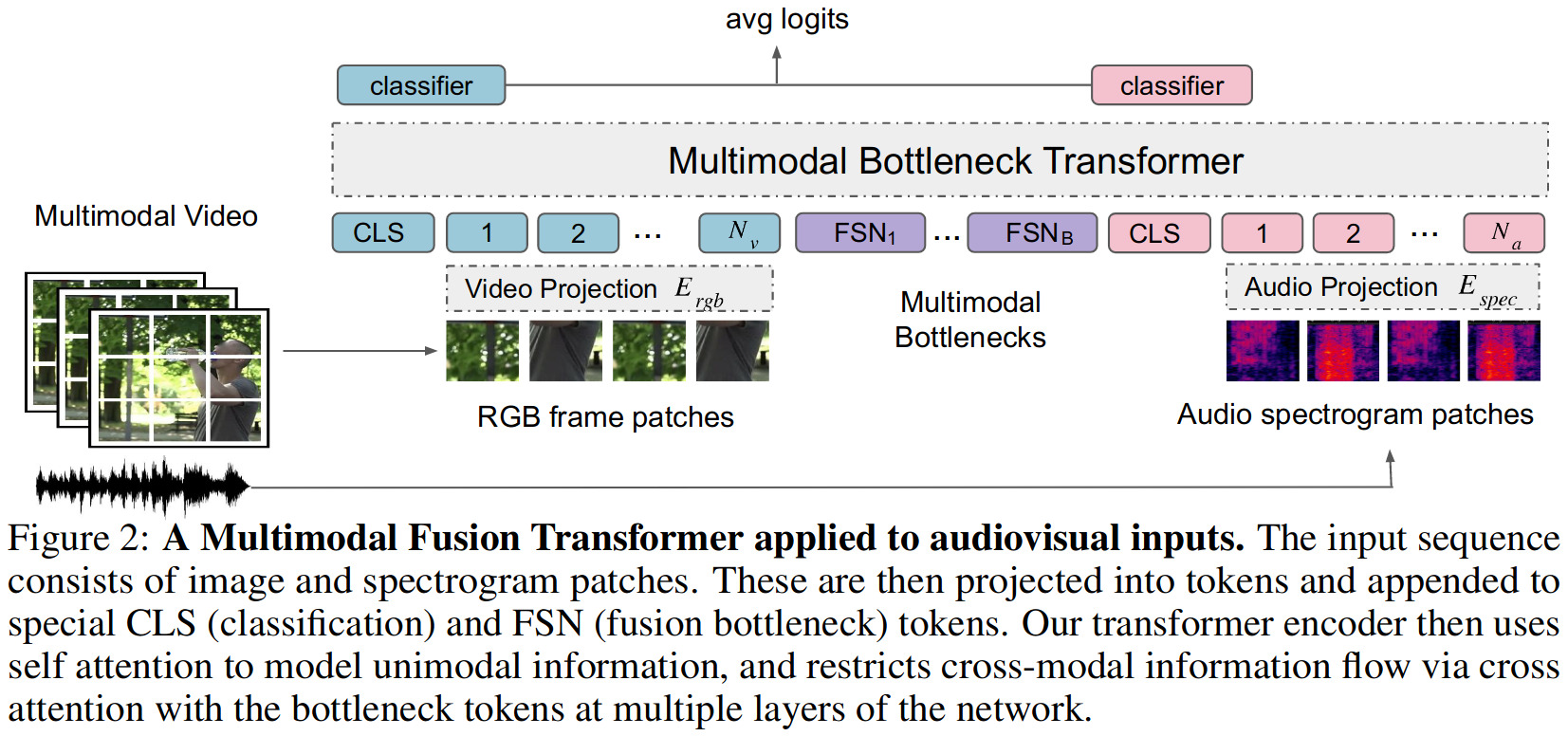
To define formally the process of attention bottlenecks, let’s first quickly redefine the classical attention mechanism as proposed by the Vision Transformer (ViT) and the Audio Spectrogram Transformer (AST).

ViT and AST attention

Let \(N\) be the number of input patches \(x_i \in \mathbb{R}^{h \times w}\). We can convert these patches into a sequence of tokens \(z_i \in \mathbb{R}^d\) using a linear projection \(\mathbf{E} \in \mathbb{R}^{d \times hw}\) and a learned positional embedding \(\mathbf{p} \in \mathbb{R}^{(N + 1) \times d}\) as follows:

\[\mathbf{z} = [z_{\text{cls}}, \mathbf{E}x_1,\mathbf{E}x_2,\dots,\mathbf{E}x_N] + \mathbf{p} \tag{1}\]

where \(z_{\text{cls}}\) denotes the class token.

The transformer layer itself, \(\text{Transformer}(\mathbf{z}^l)\), can then be defined as the composition of the following equations:

\[\mathbf{y}^l = \text{MSA}(\text{LN}(\mathbf{z}^l)) + \mathbf{z}^l \tag{2}\] \[\mathbf{z}^{l+1} = \text{MLP}(\text{LN}(\mathbf{y}^l)) + \mathbf{y}^l \tag{3}\]

where Multi-headed Self-Attention (MSA) can be defined as a function of an input \(\mathbf{X}\) as follows:

\[\text{MSA}(\mathbf{X}) = \text{Attention}(\mathbf{W}^Q\mathbf{X}, \mathbf{W}^K\mathbf{X}, \mathbf{W}^V\mathbf{X}). \tag{4}\]

Modality-specific parameters + cross-attention

The authors propose a baseline multi-modal transformer which lets each modality have its own set of parameters, and mixes information between modalities using cross attention rather than self-attention.

Given the definition of attention from the previous section, this method follows the same attention pipeline, but with one transformer model per modality and with Eq. 2 replaced by:

\[\mathbf{y}^l_{\text{mod}_i} = \text{MCA}(\text{LN}(\mathbf{z}^l_{\text{mod}_i}), \text{LN}(\mathbf{z}^l)) + \mathbf{z}^l_{\text{mod}_i} \tag{5}\]

where the \(\text{mod}_i\) subscript denote tokens, parameters, etc. that are specific to one modality.

Given the earlier definition of MSA, the MCA operation from Eq. 5 can be defined as:

\[\text{MCA}(\mathbf{X},\mathbf{Y}) = \text{Attention}(\mathbf{W}^Q\mathbf{X}, \mathbf{W}^K\mathbf{Y}, \mathbf{W}^V\mathbf{Y}). \tag{6}\]

Attention bottlenecks

As described earlier, the bottleneck comes in the form of a small set of \(B\) fusion tokens \(\mathbf{z}_{\text{fsn}} = [z_{\text{fsn}}^1,z_{\text{fsn}}^2,\dots,z_{\text{fsn}}^B]\) that are inserted in the input sequence so that it becomes like this:

\[\mathbf{z} = [\mathbf{z}_{\text{mod}_1} || \mathbf{z}_{\text{fsn}} || \mathbf{z}_{\text{mod}_2}]. \tag{7}\]

In this case, computing the next layer’s tokens becomes:

\[[ \mathbf{z}_i^{l+1} || \mathbf{\hat{z}}_{\text{fsn}_i}^{l+1} ] = \text{Transformer}([ \mathbf{z}_i^l || \mathbf{\hat{z}}_{\text{fsn}_i}^l ]; \theta_{\text{mod}_i}) \tag{8}\] \[\mathbf{z}_{\text{fsn}}^{l+1} = \text{Avg}_i(\mathbf{\hat{z}}_{\text{fsn}_i}^{l+1}) \tag{9}\]

where \(\mathbf{\hat{z}}_{\text{fsn}_i}\) are temporary fusion tokens that are discarded after they’re reduced across modalities to compute the next fusion tokens.

Bottleneck tokens are initialized using a Gaussian similar to the one used for positional embeddings. At the very end, a single output is obtained by feeding the class tokens for each modality to the same linear classifier and then averaging the pre-softmax logits across modalities.

Data

The authors test their methods on audio-video datasets:

  • AudioSet: 2 million 10-second video clips, annotated with 527 audio-event classes;
  • EpicKitchens 100: 90K variable length clips totalling 100 hours, annotated with action labels composed of a verb and noun
  • VGGSound: 200K 10-second video clips, annotated with 309 sound classes.

Results

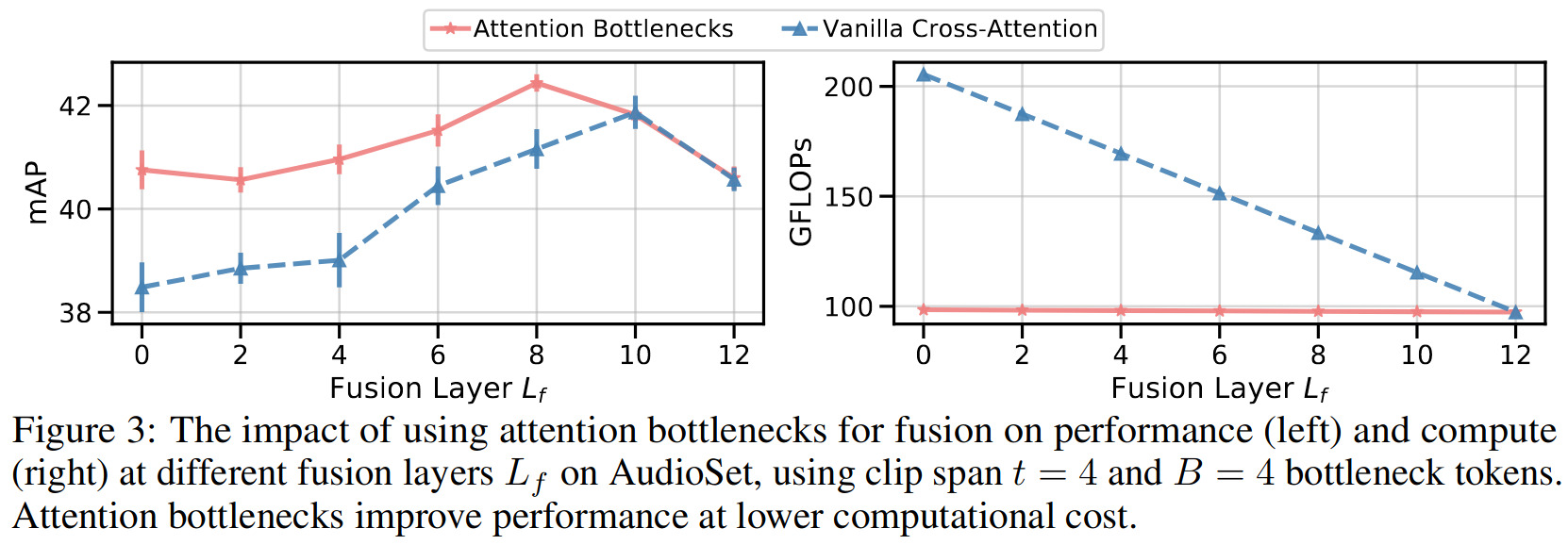
The authors report results for three different fusion strategies:

  1. Vanilla self-attention
  2. Vanilla cross-attention with separate weights
  3. Bottleneck fusion

The authors also detail the impact of many other parameters, i.e. video clip length (since videos are clipped+sampled), number of training samples, etc. on the model’s performance.

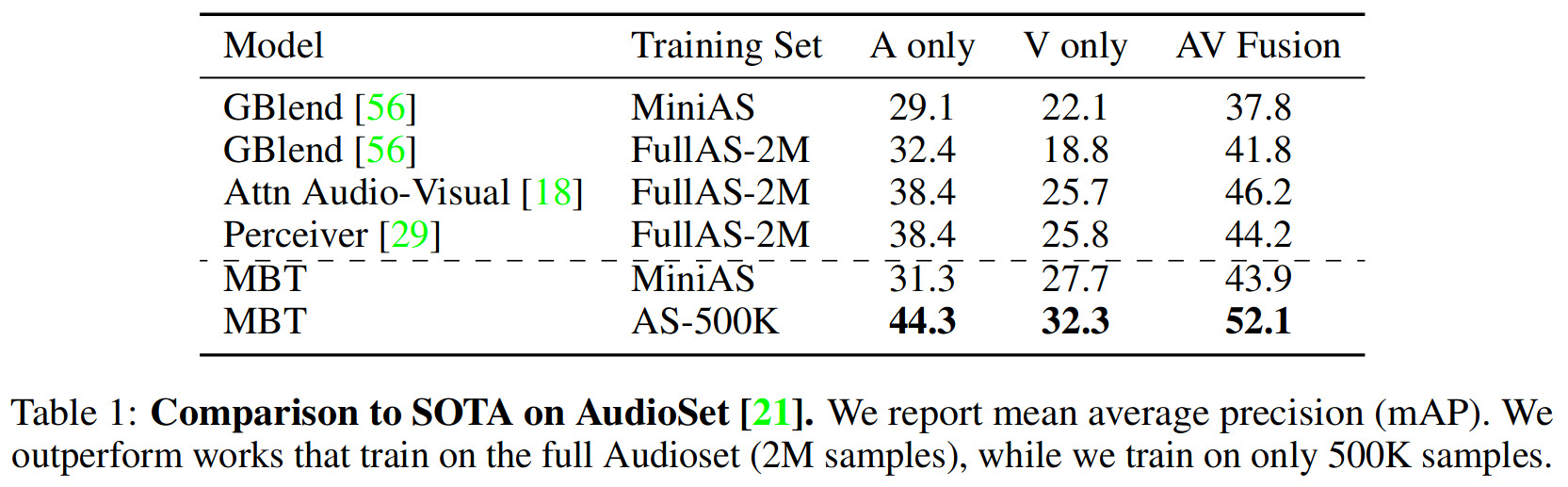
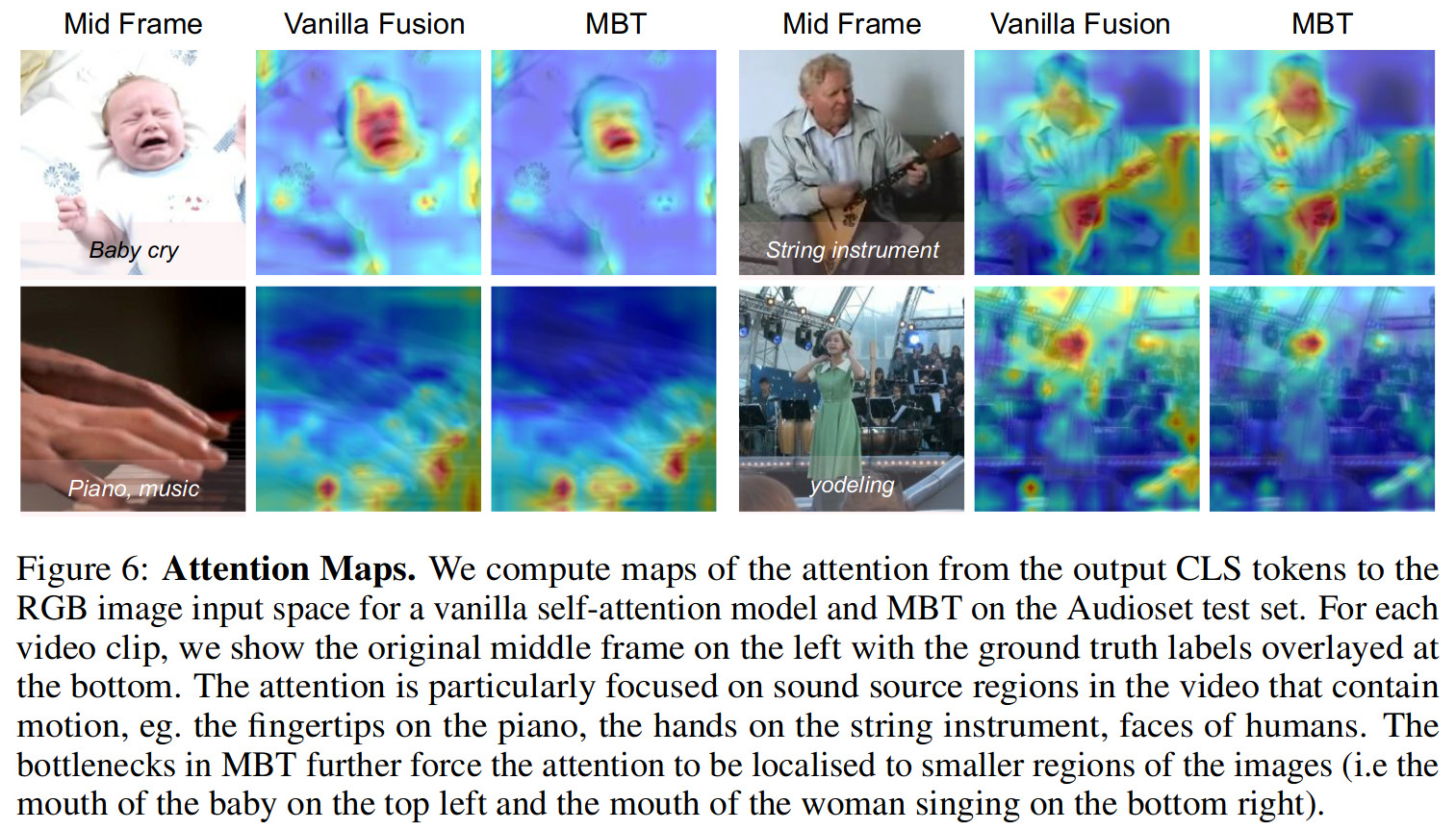
For brevity, we only include here the scores for the better-known AudioSet dataset:

References

  1. Vaswani et al., “Attention is All you Need”, NeurIPS, 2017 ↩

  2. Jaegle et al. “Perceiver: General Perception with Iterative Attention”, ICML, 2021 + a short review of the paper ↩