Introduction

Federated learning suffers from the statistical heterogeneity between participating institutions’ datasets, incuring convergence slowdown and loss in performance of trained models compared to centralized training. In this context, federated personalization methods imply training one specialized model per institution while benefitting from the collaboration with others. The others propose a novel personalization method for classification based on the definition of federated and local weights in each layer of a convolutional neural network.

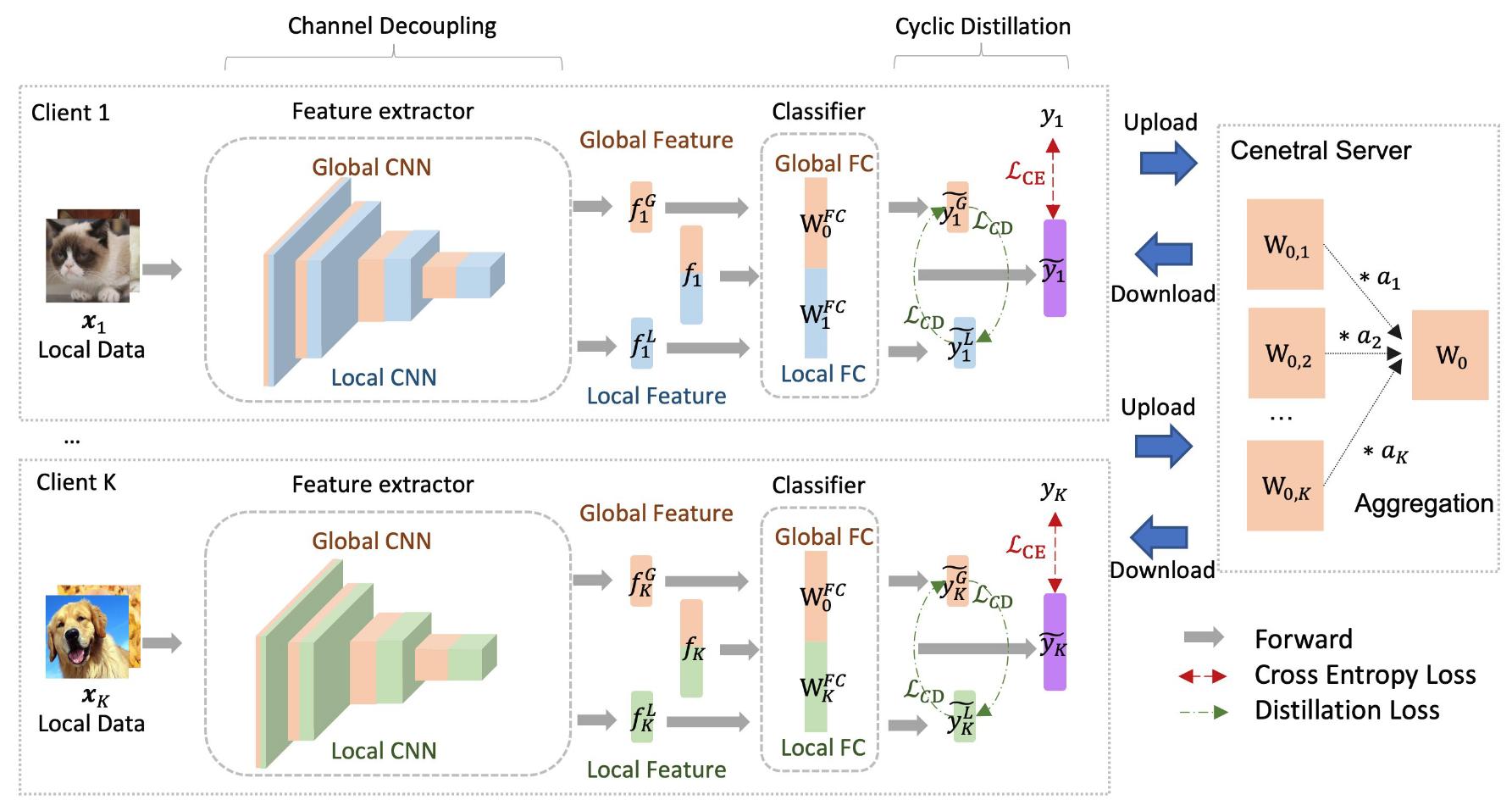
Channel decoupling

Contrarily to known methods choosing which layers of a convolutional network to federate and which to keep local, the authors propose a vertical split, with federated and private weights in each layer.

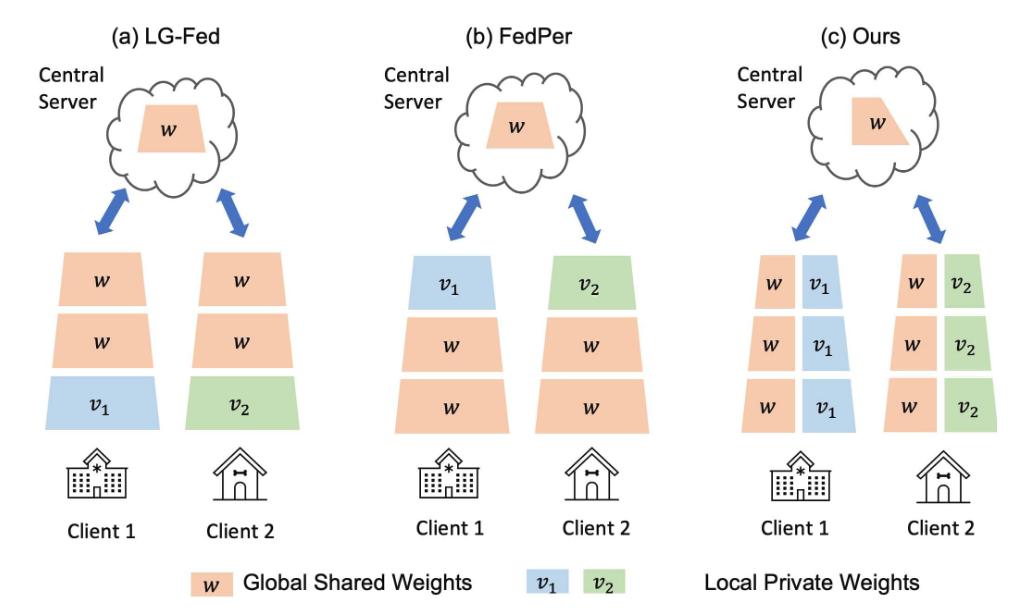
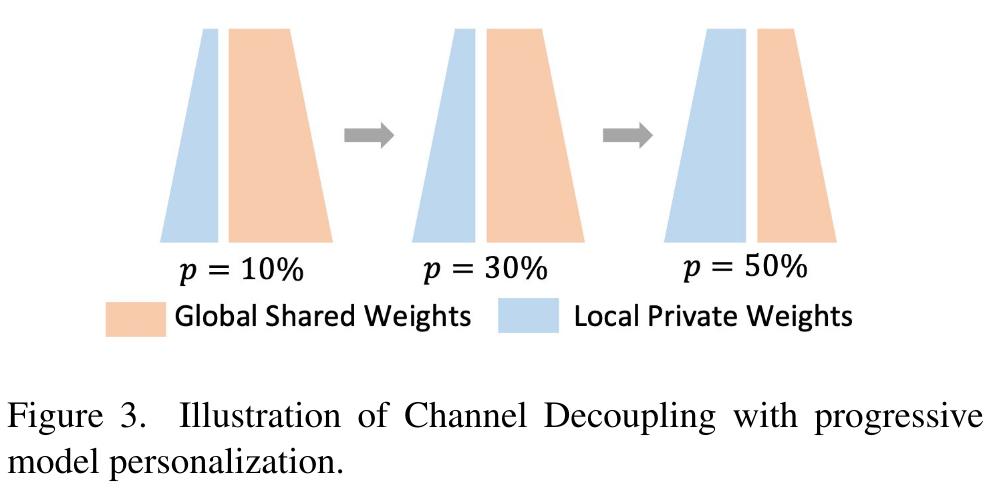
Progressive personalization

The proportion of weights per layer kept local is noted \(p\).

  • Equivalent to Fedavg when p = 0 (no personalization),
  • Equivalent to local training when p = 1 (no communication).

The authors propose to progressively increase the amount of parameters kept local during training, following a linear growth from 0 to a maximal amount of personalization \(p\) as a proof of concept, while complex schemes such as cosine annealing could be studied.

Cyclic distillation

For an institution \(k\), let’s note \(w^s_k\) the shared parameters of its model, and \(w^l_k\) its private parameters. Each set of parameters defines a subnetwork, with \(w_k := (w^s_k, w^l_k)\) the complete personalized model.

Given a local sample \(x_k\) with label \(y_k\), let’s note \(\tilde{y}_k, \tilde{y}_k^s, \tilde{y}_k^l\) the prediction made with the full network, the shared subnetwork and the private subnetwork respectively.

In addition to the classical cross entropy loss, a knowledge self-distillation loss is added as the symmetric KL divergence between logits of both subnetworks

\[L_{CD} = \frac{1}{2}(KL(\tilde{y}_k^s, \tilde{y}_k^l) + KL(\tilde{y}_k^l, \tilde{y}_k^s))\]

This process is similar to the paradigm of inplace distillation, distilling knowledge from a complete network into contained small subnetworks to boost performances.

Local temporal weight averaging

To stabilize local training, they use an “exponential moving average” for their local weight update at local epoch \(t\) with a ramping \(\beta_t\) to a maximum value \(\beta\).

\[w_k^{t} = \beta_tw_k'^{t} + (1-\beta_t)w_k^{t-1}\]

Experiments

They experiment their method on a variety of tasks.

  • Local: the sample origin is known, and the correct personalized model is used,
  • New: the sample origin is unknown, and an ensemble of personalized models is used,
  • External: the sample originates from a non participating institution, and ensemble of personalized models is used.

CIFAR-10 with a small amount of class per institution

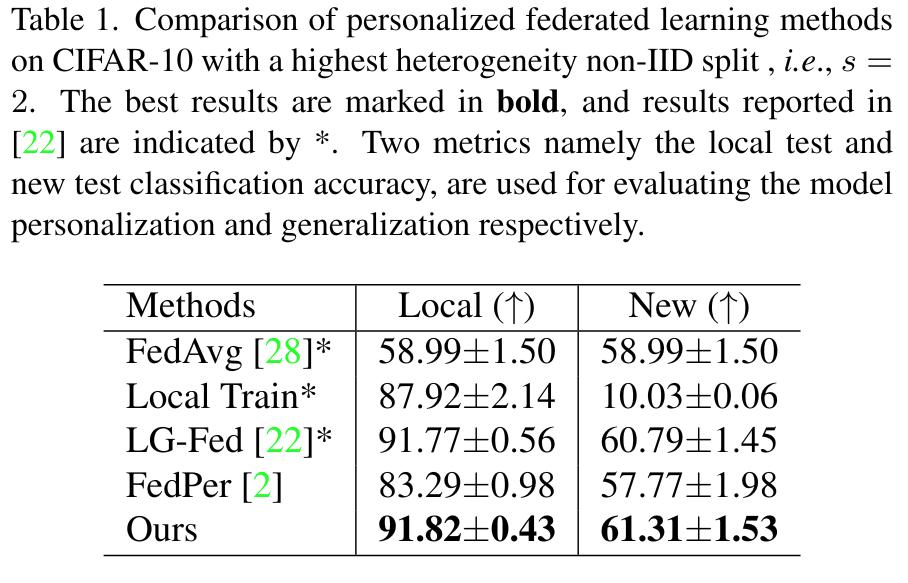
CIFAR-100 with a small amount of class per institution

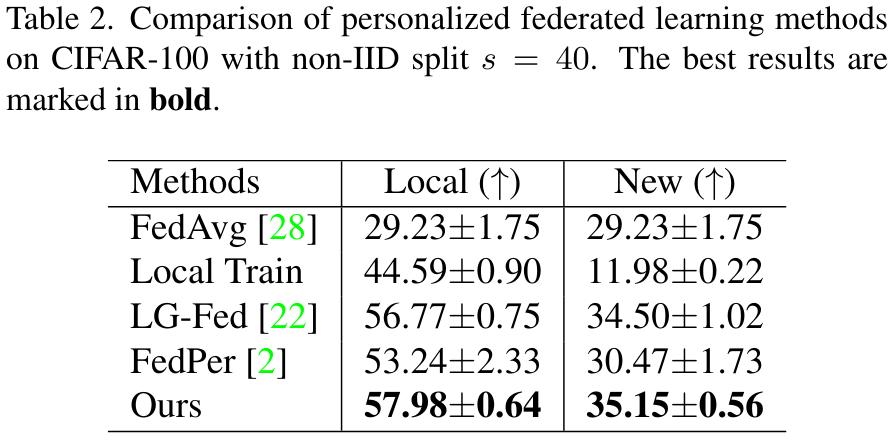
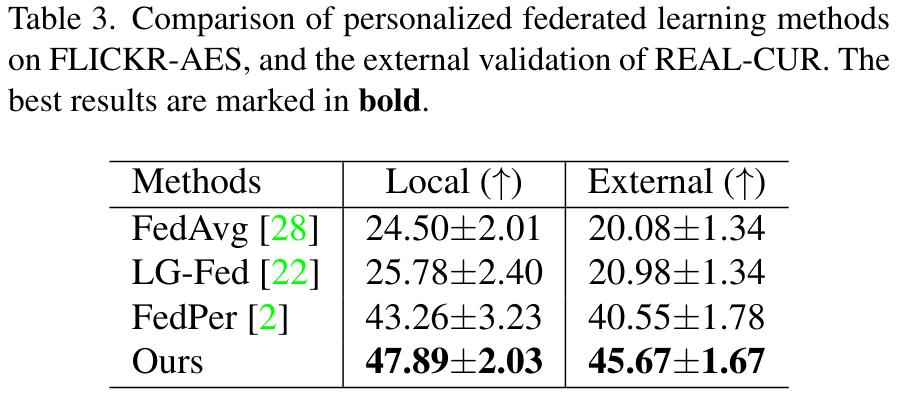
FLICKR-AES, a personal photo ranking dataset partitioned by album (implying a concept shift)

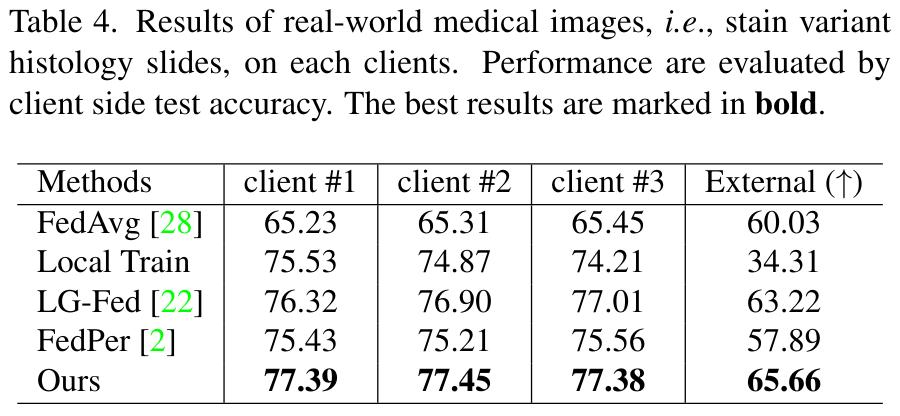
HISTO-FED, consisting of both public and private hematoxylin and eosin stained histological whole-slide images of human colorectal cancer and normal tissue (implying a strong feature shift).

Conclusion

The authors proposed a new type of parameter splitting in personalized federated learning, accompanied by several training tricks improving the performance. They tested their method on several relevant heterogeneous federated datasets for classification, showing the interest of the method.