Notes

Code is available on github

Introduction

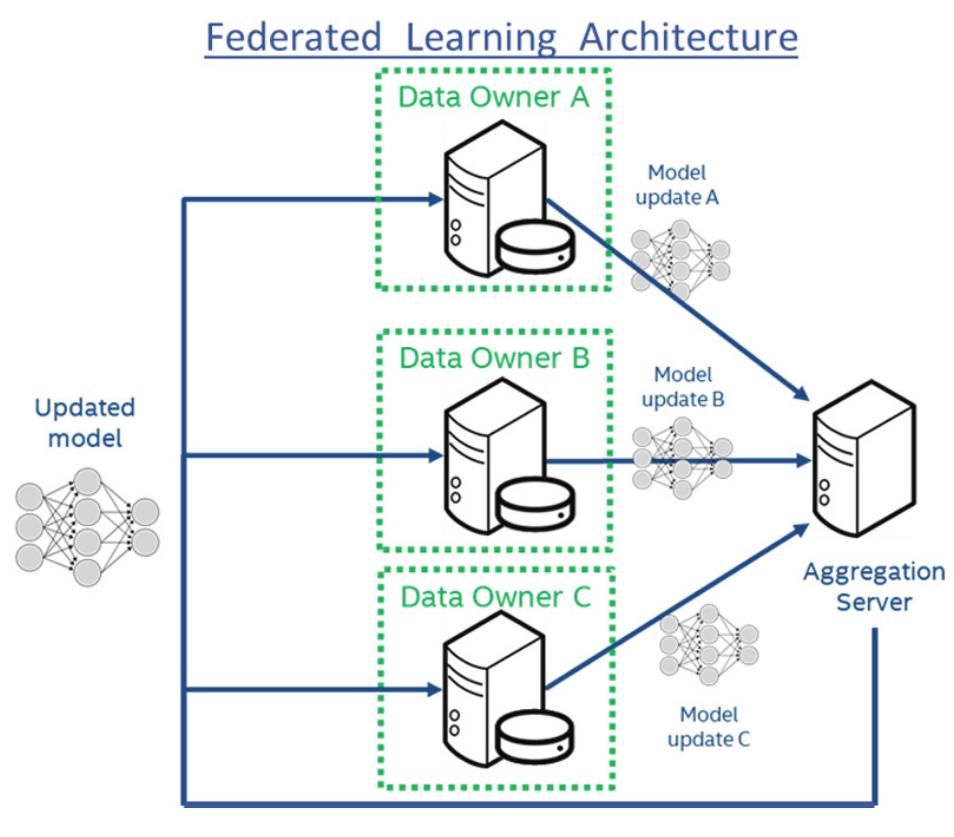
Federated learning was initially presented as a fully privacy-preserving decentralized learning paradigm, never sharing raw data between participants and the server.

Soon after its proposal, attacks designed to extract information from the transmitted local updates were developed, the most notable being Deep Leakage from Gradients¹, but working efficiently on small-sized inputs only.
The authors propose a new type of attack, Generative Gradient Leakage, leveraging external data server-side to train a generative model used to regularize a gradient inversion attack.

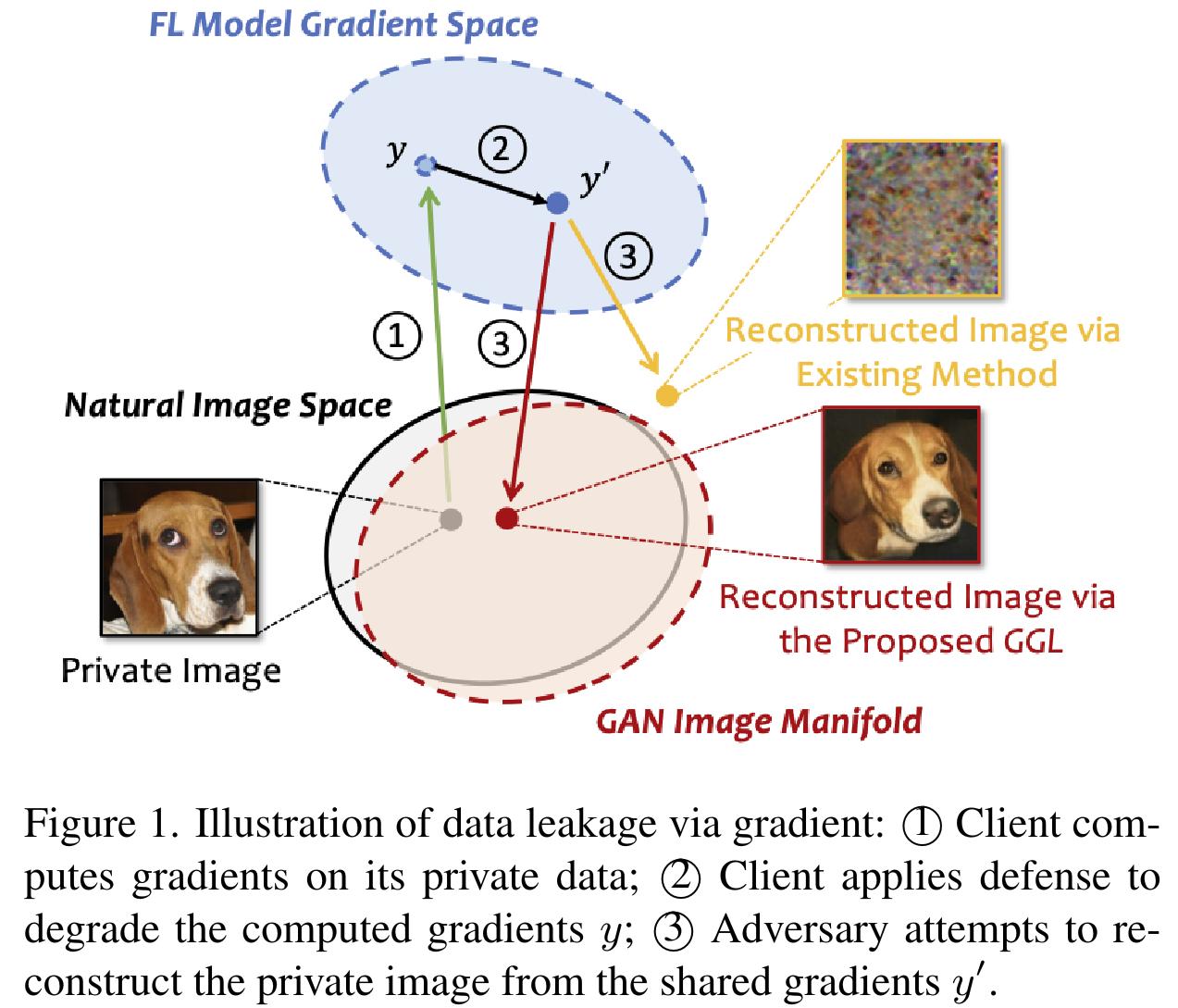
They show promising results attacking federated frameworks training on ImageNet and CelebA, reconstructing a large image from a gradient.

Overview

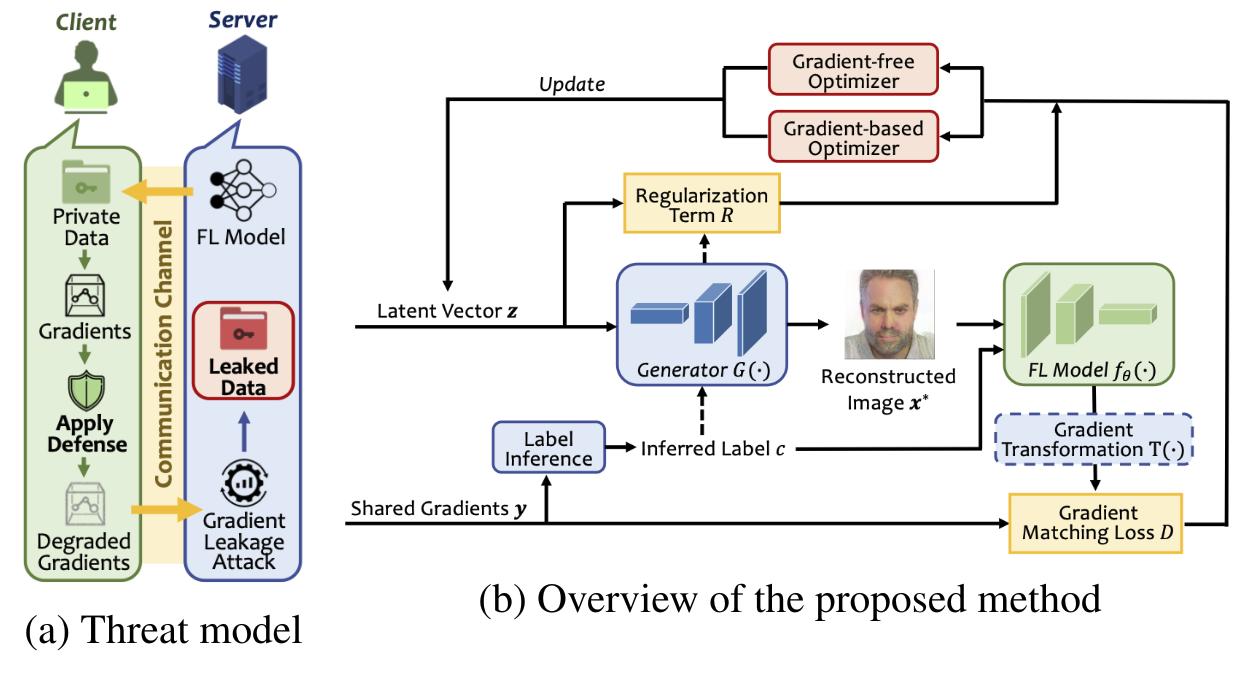
Threat model

Honest-but-curious server. It behaves normally, but will try its best to infer private information from what is accessible to it, models and degraded local updates.
Participants apply a variety of local defense mechanisms,
Access to external data server-side from the same distribution as participants.

Problem definition

Notations

\(x\in\mathbb{R}^{h\times w}\) an image with associated class label \(c\),
\(F(x)=\nabla_{\theta}\mathcal{L}(f_{\theta}(x),c)\) the gradient of \(x\) with respect to parameters \(\theta\in\mathbb{R}^p\) of a network \(f_{\theta}\),
\(y=\mathcal{T}(F(x))\) a gradient degraded by the defence transformation \(\mathcal{T}\),
\(w: \mathbb{R}^{h\times w}\rightarrow \mathbb{R}\) an image prior defining the likelihood of an image,
\(\mathcal{D}: \mathbb{R}^p\times\mathbb{R}^p\rightarrow \mathbb{R}\) a distance metric between gradients,
\(G: \mathbb{R}^k\rightarrow \mathbb{R}^{h\times w}\) a generative network trained on external data server-side,
\(\mathcal{R}(G;z)\) a regularization term, penalizing latent vector \(z\) when deviating from the prior distribution.

Previous formulation¹

\[x^* = \underset{x\in\mathbb{R}^{h\times d}}{argmin\ } \underbrace{\mathcal{D}(y, F(x))}_\text{gradient matching loss} + \underbrace{\lambda \omega(x)}_\text{regularization}\]

Novel formulation

\[z^* = \underset{z\in\mathbb{R}^{k}}{argmin\ } \underbrace{\mathcal{D}(y, \mathcal{T}(F(G(z))))}_\text{gradient matching loss} + \underbrace{\lambda \mathcal{R}(G; z)}_\text{regularization}\]

Method

Analytical label inference

For networks with a fully connected classification head using sigmoid or ReLu activation functions trained with cross-entropy loss on one-hot labels, the label can be inferred through the index of the negative entry of the gradient with respect to this layer.

Gradient Transformation Estimations

Gradient Clipping: Given a perturbation \(\mathcal{T}(w, S) = w/\text{max}(1,\frac{||w||_2}{S})\), estimate the clipping bound \(S\) as the \(l_2\) norm at each layer,

Gradient Sparsification: Given a perturbation \(\mathcal{T}(w,p) = y \odot \mathcal{M}\) with \(\mathcal{M}\) a mask with pruning rate \(p\), simply estimate \(\mathcal{M}\) using the zero entries of the gradient.

Gradient Matching Losses

Squared \(l_2\) norm

\[\mathcal{D}(y, \tilde{y}) = ||y - \tilde{y}||^2_2\]

Cosine similarity

\[\mathcal{D}(y, \tilde{y}) = 1 - \frac{<y,\tilde{y}>}{||y||_2||\tilde{y}||_2}\]

Regularization Terms

KL-based regularization (with \(\mu_i\) and \(\sigma_i\) the element-wise mean and standard deviation)

\[\mathcal{R}(G;z)=-\frac{1}{2}\sum_{i=1}^k(1+\text{log}(\sigma_i^2)-\mu_i^2-\sigma_i^2)\]

Norm-based regularization

\[\mathcal{R}(G;z) = (||z||^2_2-k)^2\]

Optimization Strategies

Gradient-based

Adam

Gradient-free

Bayesian optimization (trust region BO (TuRBO))
Covariance matrix Adaptation evolution strategy (CMA-ES)

Experiments

Federated learning and attack setup

Datasets

Binary Gender Classification with CelebA, 32x32,
1000-classes Image Classification with ImageNet ILSVRC 2012, 224x224.

Models

Federated : Resnet-18,
Generative model : DCGAN for CelebA, BigGAN for ImageNet.

Data split

GAN trained on training sets of CelebA (162k) and ImageNet,
FL task performed on the validation sets.

Evaluation metrics

Mean Square Error - Image Space (MSE-I),
Peak Signal-to-Noise Ratio (PSNR),
Learned Perceptual Image Patch Similarity (LPIPS) (measured by a VGG network),
Mean Square Error - Representation Space (MSE-R) (the feature vector before the final classification layer)

Defence schemes

Additive Noise: inject a Gaussian noise \(\epsilon \sim \mathcal{N}(0,\sigma^2I)\) to the gradients with \(\sigma = 0.1\),
Gradient Clipping: clip the values of the gradients with a bound of \(S = 4\),
Gradient Sparsification: perform magnitude-based pruning on the gradients to achieve 90% sparsity,
Soteria: gradients are generated on the perturbed representation with a pruning rate of 80%.

Results

Losses and regularizations

Squared \(l_2\) norm with KLD regularization used in further experiments.

Optimizers

The numbers of updates are set to 2500, 1000, and 800 for Adam, BO and CMA-ES respectively.

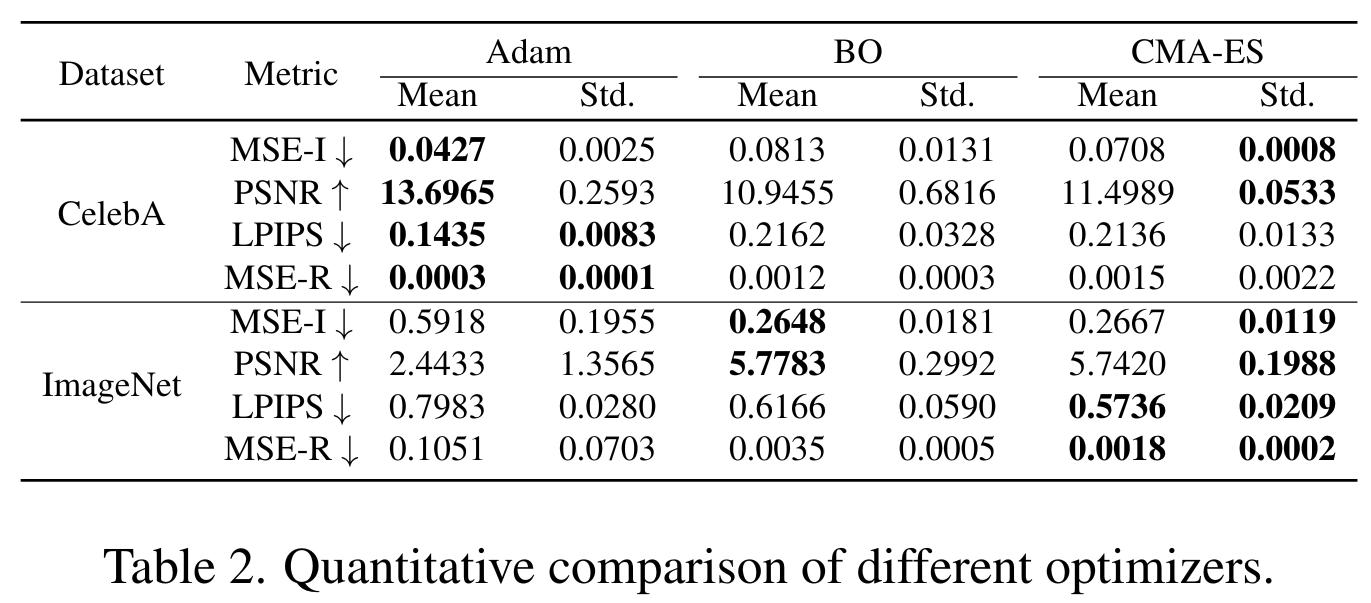
Adam works better for CelebA (aligned images), but struggles for ImageNet, highly dependent of the initialization.
CMA-ES works better for ImageNet, finding good latent vectors in the high dimensional latent space of the trained GAN.

Comparison to SOTA and effect of defences

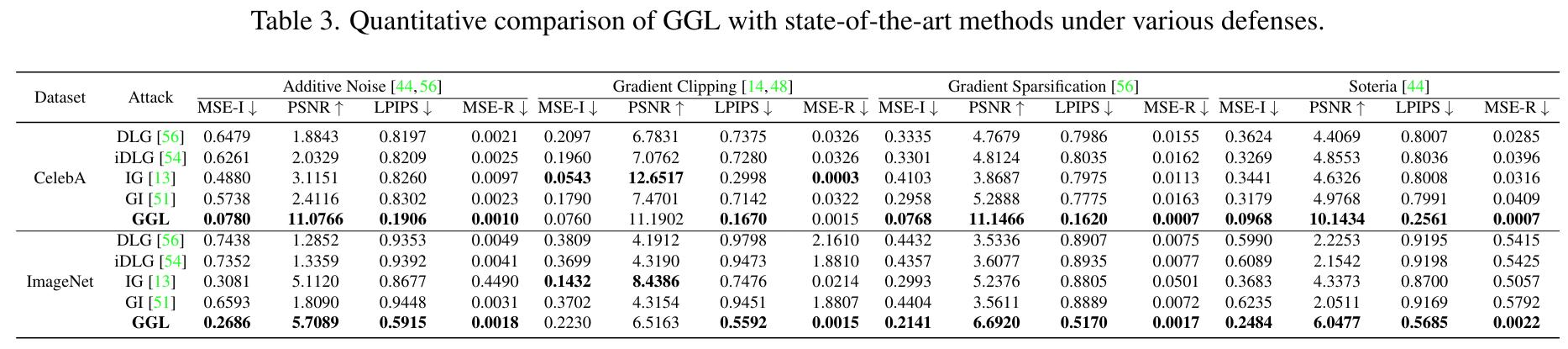
Clearly outperforms previous reconstruction attacks on all metrics and most defence mechanisms,
It is limited by the trained GAN, requiring a high amount of public or “leaked” data and hard-constraining the reconstructed image to be generatable by GAN.

Conclusion

The authors show promising results attacking federated frameworks training on ImageNet and CelebA, reconstructing a large image from a gradient.
This work must be seen as a valuable proof of concept: the assumptions are extremely strong, limiting its applicability in real contexts, but the idea is quite appealing, opening a whole new spectrum of gradient inversion techniques.

References

Ligeng Zhu et al, Deep Leakage from Gradients ↩ ↩²