Notes

Code is available on this GitHub repo

Highlights

Diffusion models (DMs) are applied in the latent space of powerful pretrained autoencoders
Allows to reach a good compromise between complexity reduction and details preservation
Introduce cross-attention layers into the model architecture for general conditioning inputs such as text
The model significantly reduces computational requirement compared to pixel-based DMs
The model achieves new SOTA for image inpainting and class-conditional image synthesis
The model achieves highly competitive results on text-to-image synthesis, unconditional image generation and super-resolution

Introduction

DMs are computationally demanding since it requires repeated function evaluation in the high-dimensional space of RGB images

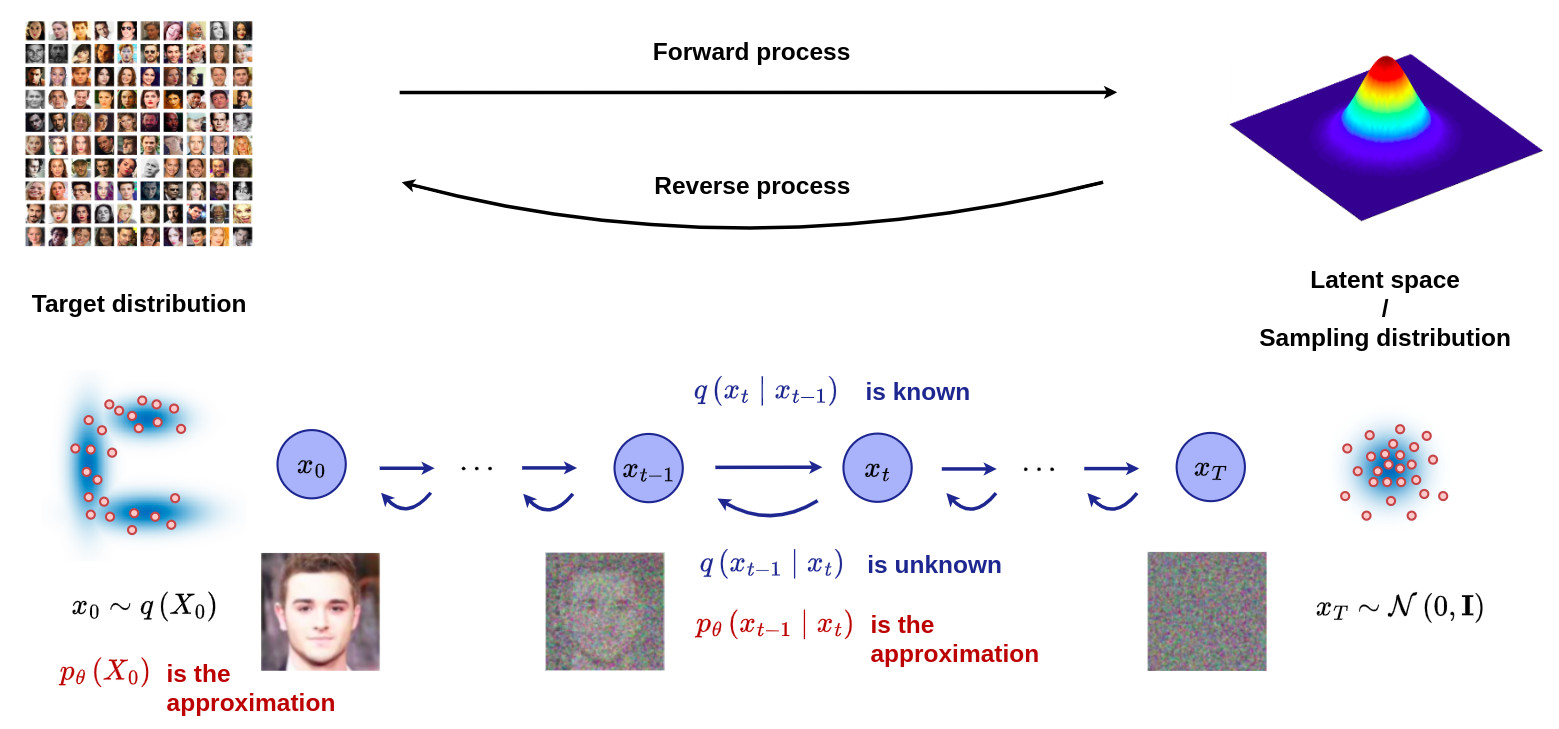
See the tutorial on DDPM for more information.

The figure below shows the rate-distorsion trade-off of a trained model. Learning can be divided into two stages:

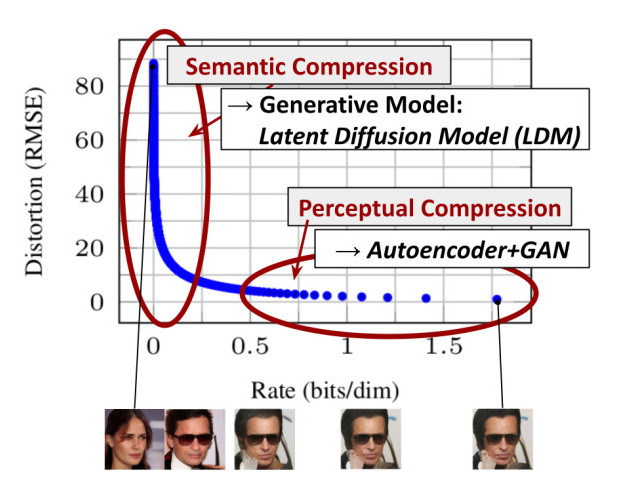
Figure 1. Illustrating perceptual and semantic compression.

Most bits of a digital image correspond to imperceptible details, leading to unnecessary expensive optimization and inference

If a latent space without imperceptible details can be learned independently, DMs can then be applied efficiently from this space to only focus on semantic properties

Methodology

Perceptual image compression

A perceptual compression model based on previous work [1] is used to efficiently encode images
It consists in an auto-encoder trained by combinaison of a perceptual loss and a patch-based adversarial objective
The overall objective of the cited paper is more complex than only computing an efficient latent space (high-resolution image synthesis based on transformer), but as far as I understand the pre-trained encoder/decoder parts are available and directly used in latent DM formalism. This paper should be the subject of a future post!
two different kinds of regularizations are tested to avoid high-variance latent spaces: KL-reg which imposes a slight KL-penality towards a standard normal on the learned latent space, and VQ-reg which uses a vector quantization layer [2] within the decoder.

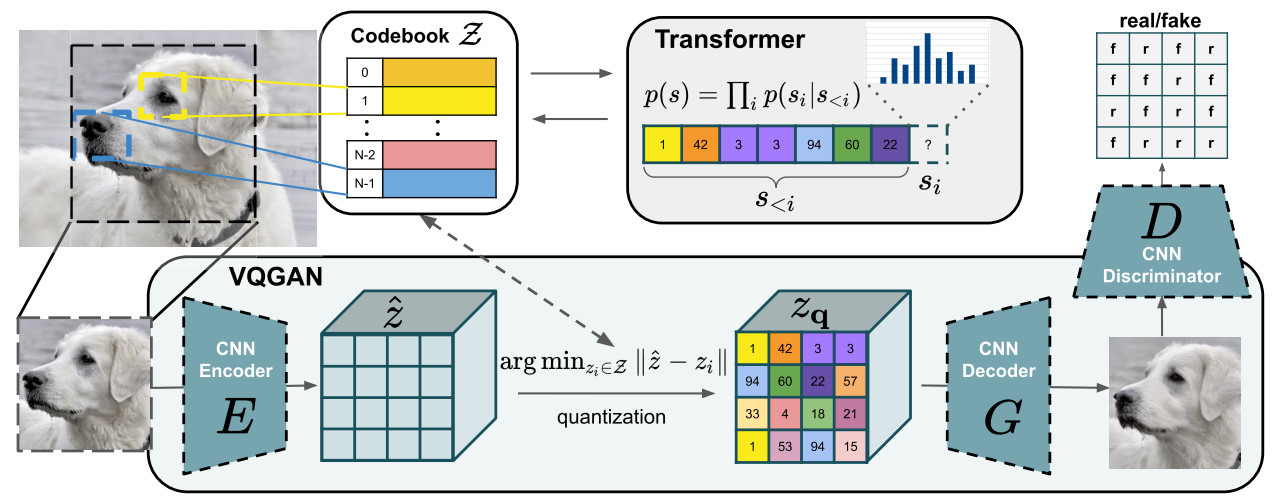
Figure 2. Illustration of the perceptual compression model detailed in [1] and used to compute the encoder/decoder module.

Model architecture

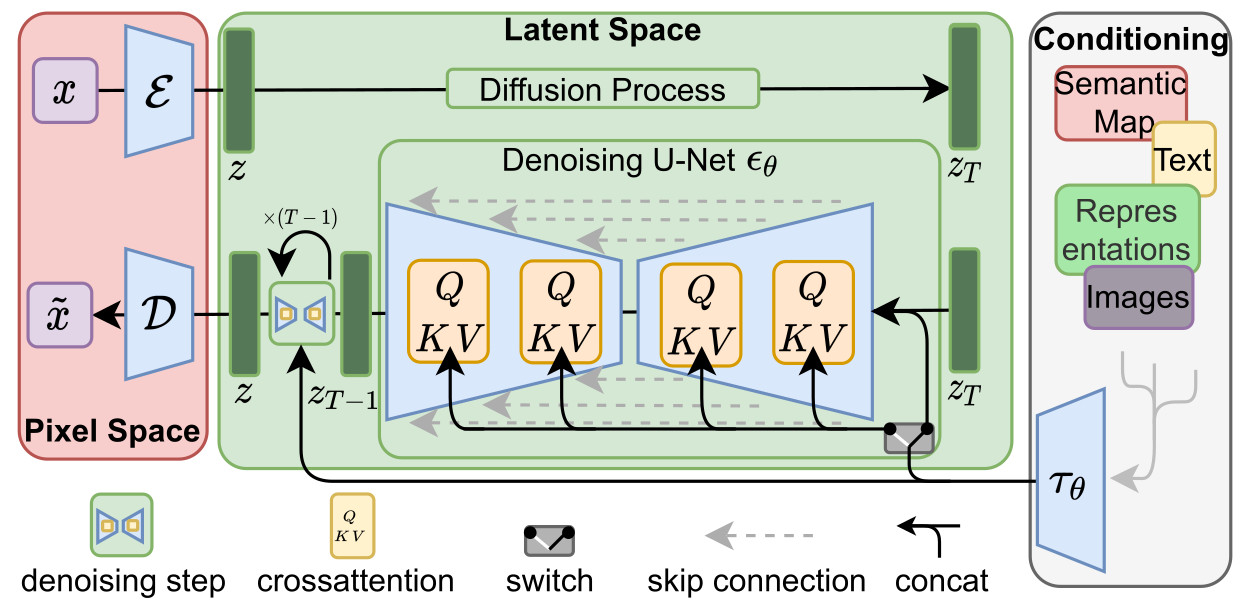
The latent diffusion model is composed of 3 main parts:

an encoder \(E\) / decoder \(D\) module which allows to go from the pixel space to a latent space which is perceptually equivalent, but offers significantly reduced computational complexity
a time-conditional U-Net for the denoising parts \(\epsilon_{\theta}(z_t,t)\).
a conditioning module to efficiently encode and propagate an additional source of information \(y\) through cross-attention mechanisms

The learning of the LDM without the cross-attention module can be modeled as:

\[\mathcal{L}_{LDM} := \mathbb{E}_{z \sim E(x), \epsilon \sim \mathcal{N}(0,\mathbf{I}), t \sim [1,T]} \left[ \| \epsilon_t - \epsilon _{\theta}(z_t,t)\|^2 \right]\]

Conditioning mechanisms

a domain specific encoder \(\tau_{\theta}\) that projects \(y\) to an intermediate representation \(\tau_{\theta}(y)\) is introduced
this intermediate representation is then mapped to the intermediate layers of the Unet via a cross-attention layer as illustrated below:

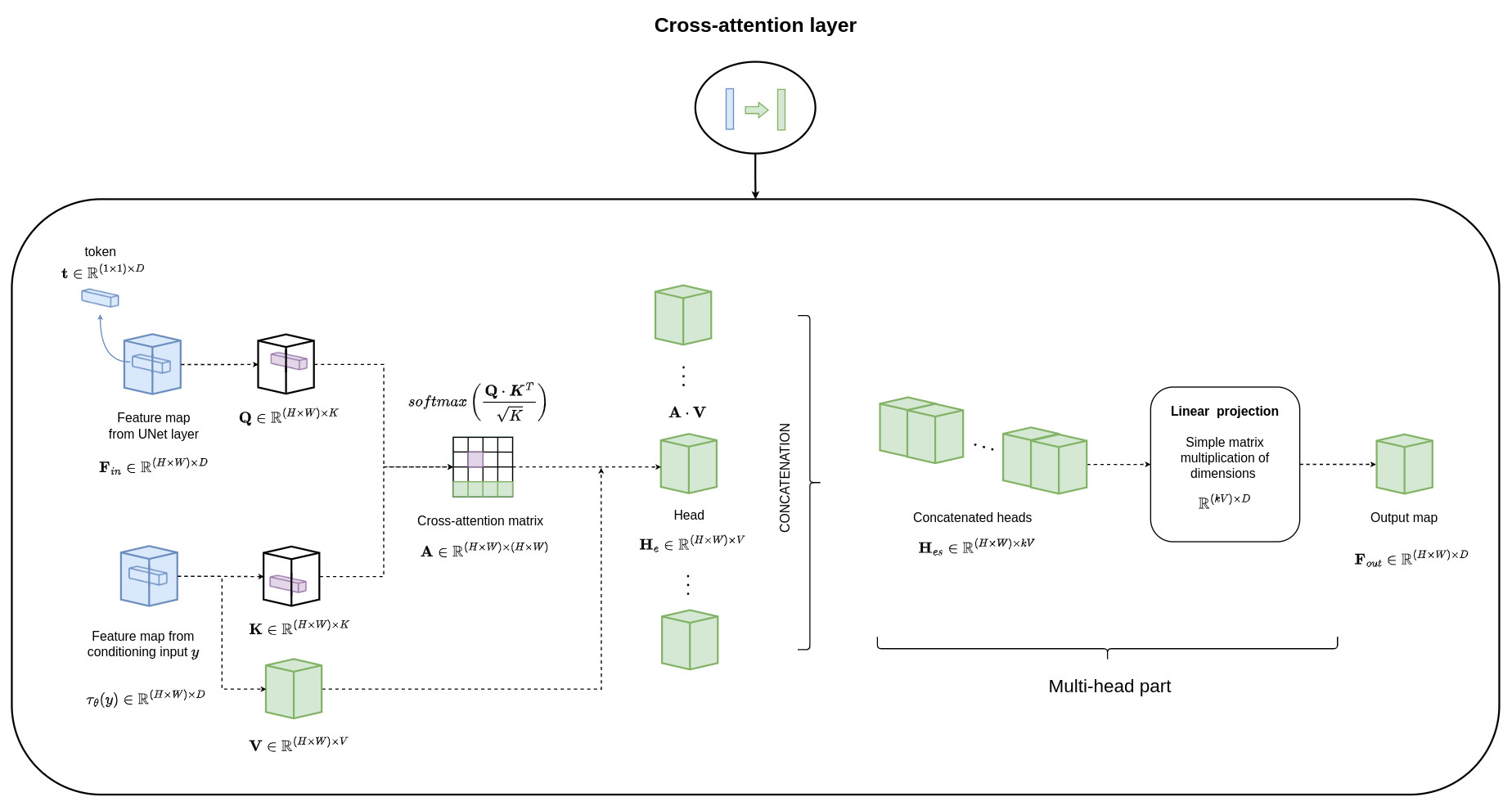
The learning of the LDM with the cross-attention module can be modeled as:

\[\mathcal{L}_{LDM} := \mathbb{E}_{z \sim E(x), y, \epsilon \sim \mathcal{N}(0,\mathbf{I}), t \sim [1,T]} \left[ \| \epsilon_t - \epsilon _{\theta}(z_t,t,\tau_{\theta}(y))\|^2 \right]\]

Results

6 different kinds of image generation: text-to-Image, Layout-to-Image, Class-Label-to-Image, Super resolution, Inpainting, Semantic-Map-to-Image
Latent space with 2 different regularization strategies: KL-reg and VQ-reg
Latent space with different degrees of downsampling
LDM-KL-8 means latent diffusion model with KL-reg and a downsampling of 8 to generate the latent space
DDIM is used during inference (with different number of iterations) as an optimal sampling procedure
FID (Fréchet Inception Distance): captures the similarity of generated images to real ones better than the more conventional Inception Score

Perceptual compression tradeoffs

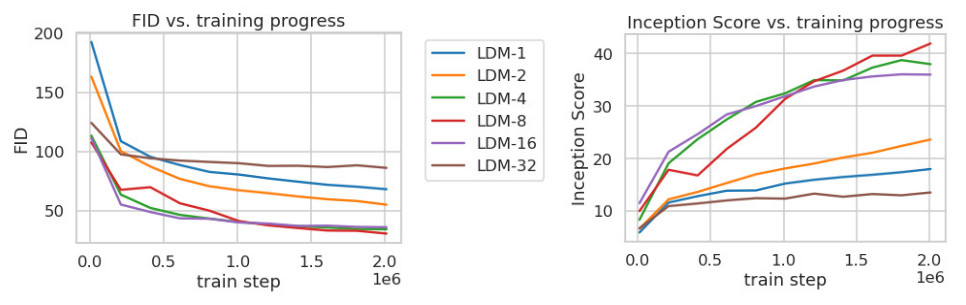
Figure 3. Analyzing the training of class-conditional LDMs with different downsampling factors f over 2M train steps on the ImageNet dataset.

LDM-1 corresponds to DM without any latent representation
LDM-4, LDM-8 and LDM-16 appear to be the most efficient
LDM-32 shows limitations due to high downsampling effects

Hyperparameters overview

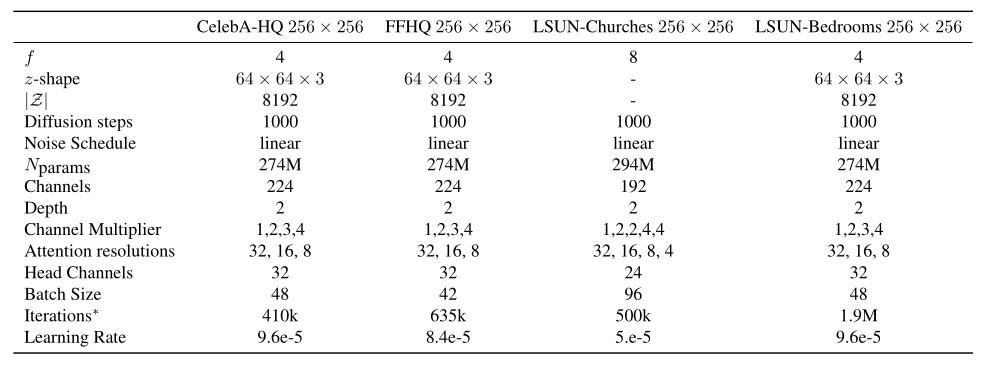
Table 1. Hyperparameters for the unconditional LDMs producing the numbers shown in Tab. 3. All models trained on a single NVIDIA A100.

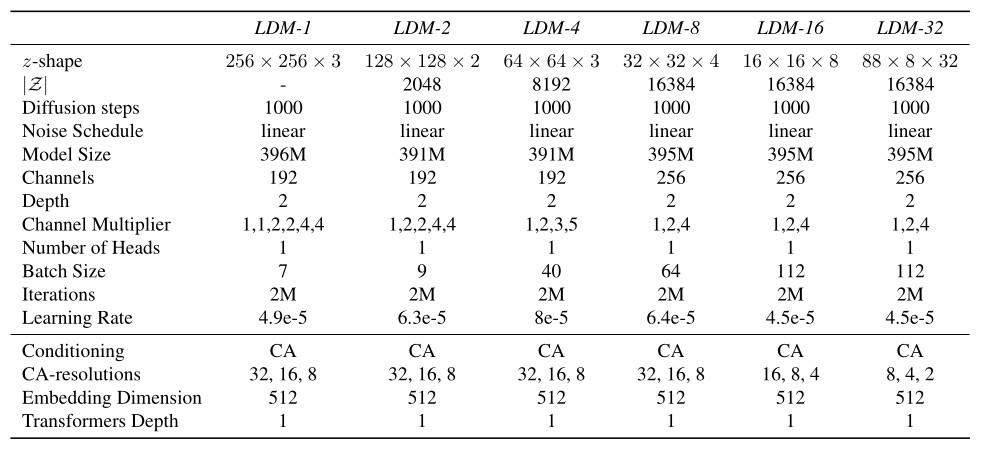
Table 2. Hyperparameters for the conditional LDMs trained on the ImageNet dataset. All models trained on a single NVIDIA A100.

Unconditional image synthesis

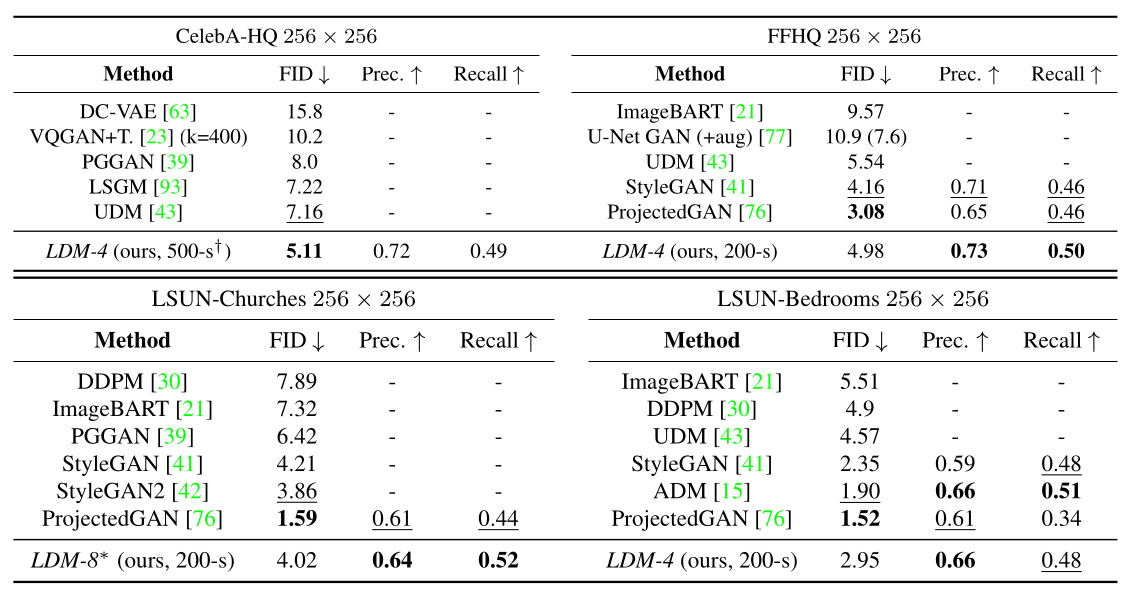
Table 3. Evaluation metrics for unconditional image synthesis. N-s refers to N sampling steps with the DDIM sampler. ∗: trained in KL-regularized latent space

Figure 4. Random samples of the best performing model LDM-4 on the CelebA-HQ dataset. Sampled with 500 DDIM steps (FID = 5.15)

Figure 5. Random samples of the best performing model LDM-4 on the LSUN-Bedrooms dataset. Sampled with 200 DDIM steps (FID = 2.95)

Class-conditional image synthesis

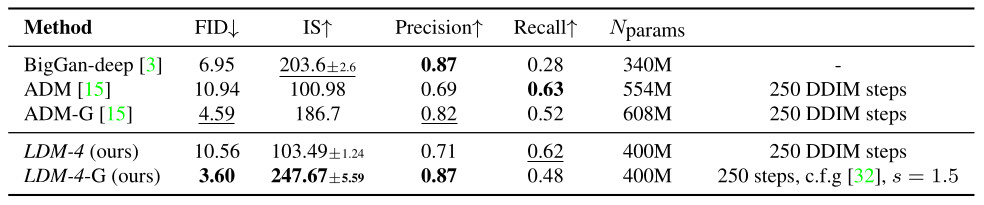
Table 4. Comparison of a class-conditional ImageNet LDM with recent state-of-the-art methods for class-conditional image generation on ImageNet. c.f.g. denotes classifier-free guidance with a scale s

Figure 6. Random samples from LDM-4 trained on the ImageNet dataset. Sampled with classifier-free guidance scale s = 5.0 and 200 DDIM steps

Text-conditional image synthesis

a LDM with 1.45B parameters is trained using KL-regularized conditioned on language prompts on LAION-400M
use of the BERT-tokenizer
\(\tau_{\theta}\) is implemented as a transformer to infer a latent code which is mapped into the UNet via (multi-head) cross-attention

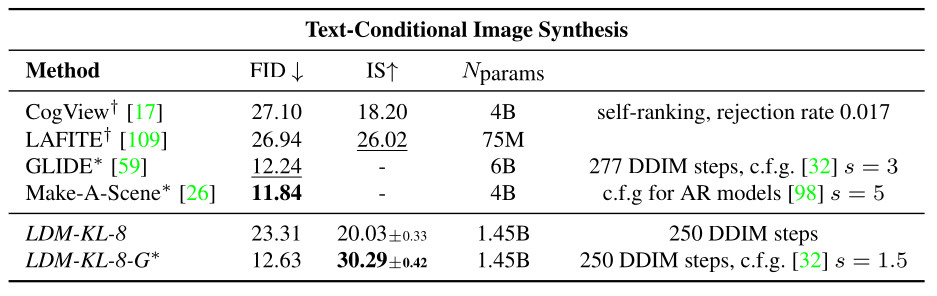
Table 5. Evaluation of text-conditional image synthesis on the 256×256-sized MS-COCO dataset: with 250 DDIM steps

Figure 7. Illustration of the text-conditional image synthesis. Sampled with 250 DDIM steps

Semantic-map-to-image synthesis

Use of images of landscapes paired with semantic maps
Downsampled versions of the semantic maps are simply concatenated with the latent image representation of a LDM-4 model with VQ-reg.
No cross-attention scheme is used here
The model is trained on an input resolution of 256x256 but the authors find that the model generalizes to larger resolutions and can generate images up to the megapixel regime

Figure 8. When provided a semantic map as conditioning, the LDMs generalize to substantially larger resolutions than those seen during training. Although this model was trained on inputs of size 256x256 it can be used to create high-resolution samples as the ones shown here, which are of resolution 1024×384

Conclusions

Latent diffusion model allows to synthesize high quality images with efficient computational times.
The key resides in the use of an efficient latent representation of images which is perceptually equivalent but with reduced computational complexity

References

[1] P. Esser, R. Rombach, B. Ommer, Taming transformers for high-resolution image synthesis, CoRR 2022, [link to paper]

[2] A. van den Oord, O. Vinyals, and K. Kavukcuoglu, Neural discrete representation learning, In NIPS, 2017 [link to paper]