Self-supervised Feature Learning for 3D Medical Images by Playing a Rubik’s Cube

Highlights

• Presentation of a self-supervised pretext task for 3D medical images
• Learning of translational and rotation invariant features from raw 3D data
• Proven efficiency in classification or segmentation tasks

Introduction

There is a lot of 3D data available in hospitals, but annotating it to train deep learning algorithms is very costly. One of the solutions proposed to take advantage of all this data is self-supervised learning. The goal is to pre-train a network on a large unannotated dataset by learning a pretext task, and then fine-tune it for the target task with the reduced annotated dataset.

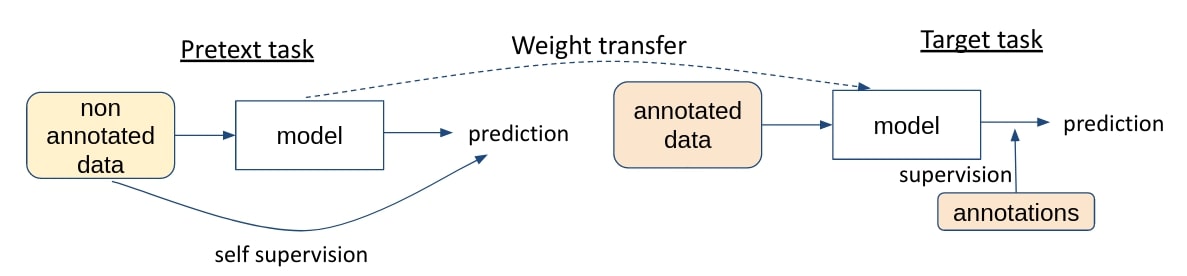
Classical pretext tasks are grayscale image colorization, inpainting or jigsaw puzzle among others. This article proposes for the first time a task specific to 3D data, inspired by the Rubik’s cube.

Method

Data preprocessing

The proposed task enforces the network to learn the translation and rotation invariant features from the raw data, as it involves both cube rearrangement and cube rotation.

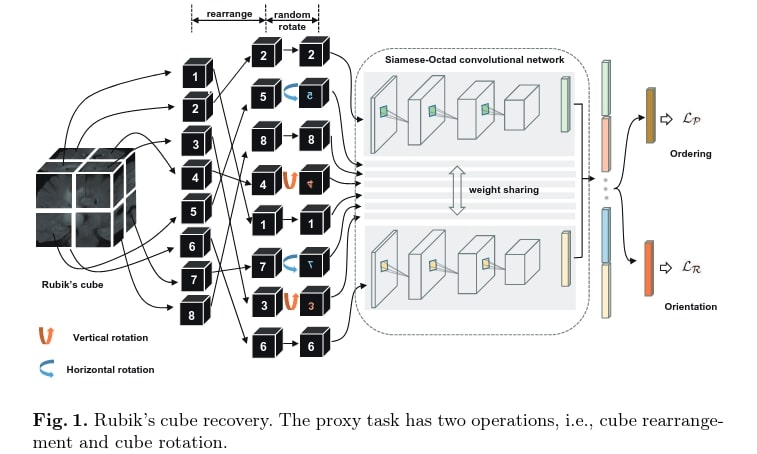
The method is inspired by the jigsaw puzzle pretext task, but adapted to 3D medical images by adding some rotations to increase the difficulty. The first step is to separate the volume into cubes, which are then rearranged and randomly rotated. Since the goal is to learn high-level semantic features and not texture information close to cubes boundaries, a gap of “about 10 voxels” is left between two adjacent cubes. Each cube is also normalized to [-1,1].

Network architecture

\(M\) siamese networks with shared weight branches, that they call Siamese-Octad, are used to solve the problem, with \(M\) being the number of cubes. The backbone can be any 3D CNN. The feature maps of the last layer of all branches are concatenated and given to a last fully connected layer for the two tasks and supervised by permutation loss and rotation loss.

Cube ordering

As there are \(M!\) permutations and that some may be very close to each other, too ambiguous and challenging to distinguish, they iteratively select \(K\) permutations with the largest Hamming distance. The network is then trained to recognize which one of the \(K\) permutations has been applied to the input volume: it is a classification task with \(K\) categories. With \(p\) the network prediction and \(l\) the one-hot label, the loss is defined as

\[L_p = - \sum{l_j \log p_j}\]

Cube orientation

In order not to extract only translation invariant features, they add some rotation. For each cube there could be 3 (axes) * 2 (directions) * 4 (angles) = 24 configurations. Again, to reduce the complexity, they limited the modifications to 180° horizontal and vertical rotations. The network has to recognize whether each cube has been rotated or not: it is a multi-label classification task with two \(1*M\) vectors for each direction with 1 at the position of rotated cubes and 0 otherwise as ground truth. If \(r\) are the predicted vectors and \(g\) the ground truth, the loss is

\[L_r = - \sum_i^M{g_i^{hor} \log r_i^{hor} + g_i^{ver} \log r_i^{ver}}\]

Objective

The global loss is weighted according to the importance of the two tasks.

\[L = \alpha L_p + \beta L_r\]

They experimentally found that \(\alpha = \beta = 0.5\) are the best weights.

Weights transfer

For a target classification task, the pretrained CNN can be directly fine-tuned but for a segmentation task, the weights can only be transferred to the encoder of a FCN. As the random initialization of the decoder might neutralize the improvement brought by the pretraining, they apply convolutional operations directly on the feature maps of the pre-trained encoder to obtain dense pixel-wise prediction, instead of using transposed convolutions on downsampled feature maps (i.e. traditional decoder architectures). This decoder architecture was inspired by dense upsampling convolutions, which has fewer trainable parameters in the decoder.

Results

Experimental setup

For classification: brain hemmorage classification, 1486 volumes classified between aneurysm, arteriovenous malformation, moyamoya disease and hypertension. For segmentation : BraTS-2018 with 285 volumes, the different modalities are concatenated. Data sets are randomly separated into two sets: 80% for training, 20% for testing. The architecture used for the Siamese-Octad branches is 3D VGG.

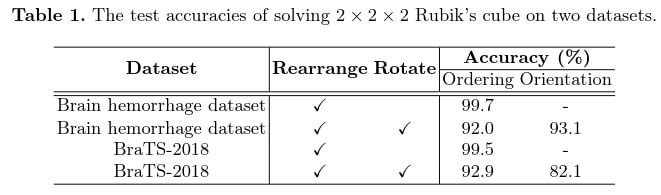
Pretext task results

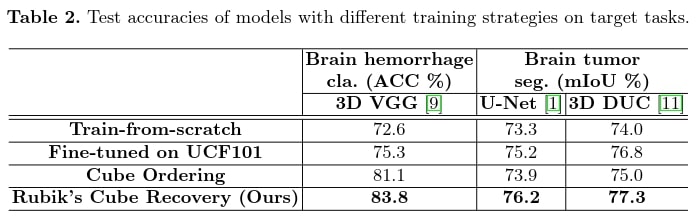
Target task results

Conclusion

The 3D Rubik’s cube pretext task gives better results for both classification and segmentation. Even if the addition of rotation reduces the performance of the classification prediction in the pretext task, the improvement of the results in the target task is greater with it, as it extracts more diverse features from the images. It would have been interesting to compare it with other classical pretext tasks that are not specific to 3D medical images. In addition, the classic application case is to use a different and larger dataset for the pretext task, which is not the case here.