Highlights

Significant site and scanner effects exist in Density Tensor Imaging (DTI) scalar maps.
Several multi-site harmonization methods are proposed.
ComBat (Combat Batch Effects) performs the best at removing site effects in diffusion metrics such as Fractional Anisotropy (FA) and Mean Diffusitivity (MD).
Voxels associated with age in FA and MD are more replicable after ComBat.
ComBat is generalizable to other imaging modalities.
A software implementing the ComBat methodology to imaging data is available in both R and Matlab on GitHub (https://github.com/Jfortin1/ComBatHarmonization).
An extensive evaluation and comparison of several methods is carefully conducted.

Introduction

Diffusion tensor imaging (DTI) is a well-established Magnetic Resonance Imaging (MRI) technique used for studying microstructural changes in the white matter. It has been shown that DTI metrics (FA, MD, …) can be used to study both brain development and pathology (Alzheimer, Parkinson, Sclerosis …) ¹.
As with many other imaging modalities, DTI images suffer from technical between-scanner variation that hinders comparisons of images across imaging sites, scanners and over time.
The authors show that the DTI measurements are highly site-specifics highlighting the need to correct for site effects before performing downstream statistical analyses. The process of correcting these site-effects is usually call harmonization.
ComBat is a popular batch-effect correction tool used in genomics.
The authors use age as a biological phenotype of interest and show that ComBat both preserves biological variability and removes the unwanted variation introduced by site. The method can be extended to more than one phenotype of interest.

Methodology

Brief overview of the materials

This study:

Considers data from two different scanners was considered, stemming from two public datasets. Only participants matching on age, gender, ethnicity and handedness were retained, resulting in 105 participants.
Presented some results for several diffusion metrics in the supplementary materials. We will mainly focus on the FA diffusion metric.

Has a fundamental Image Processing part:
- Quality control was done manually on each image of each volume, removing unwanted signal dropouts.
- All images are registered on the Eve template.
Shows the need of harmonization between sites.
Considers 5 harmonization methods including ComBat.

Datasets

Dataset 1 details (Site 1): PNC dataset: The authors selected a subset of the Philadelphia Neurodevelopmental Cohort (PNC) [Satterthwaite et al., 2014], and included 105 healthy participants from 8 to 19 years old. 83 of the participants were males (22 females), and 75 participants were white (30 non-white). The DTI data were acquired on a 3T Siemens TIM Trio whole-body scanner with the following parameters: TR = 8100 ms and TE = 82 ms, b-value of 1000 s/mm2, 7 b= 0 images and 64 gradient directions. The images were acquired at 1.875 × 1.875 × 2 mm resolution. During the same session, structural T1weighted (T1-w) MP-RAGE images were also acquired with parameters TR = 1810 ms, TE = 3.5 ms, TI = 1100 ms and FA = 9°, at 0.9375 × 0.9375 × 1 mm resolution.
Dataset 2 details (Site 2): ASD dataset: The dataset contains 105 typically developing controls (TDC) from a study focusing on autism spectrum disorder (ASD) [Ghanbari et al., 2014]. 83 of the participants were males (22 females), and 79 participants were white (26 non-white). The age of the participants ranges from 8 to 18 years old. The DTI data were acquired on a Siemens 3T Verio scanner at 2mm isotropic resolution with the following parameters: TR = 11,000 ms and TE = 76 ms, b-value of 1000 s/mm2, 1 b= 0 images and 30 gradient directions. Structural T1-w MP-RAGE images were also acquired with parameters TR = 1900 ms, TE = 2.54 ms, TI = 900 ms and FA = 9° at resolution 0.8 mm × 0.8 mm × 0.9 mm.

For benchmarking the different harmonization procedures, they use two additional subsets of the PNC database, with participants who differ from Dataset 1:

Independent Dataset 1: The dataset contains 292 additional healthy participants from the PNC with the same age range as Dataset 1 and Dataset 2 (8 to 18 years old).
Independent Dataset 2: The dataset contains 105 additional healthy participants from the PNC with an age range of 14 to 22 years old.

Image processing

Quality control on diffusion weighted images was performed manually. For each DWI volume, the authors removed weighted gradient images exhibiting signal dropout likely caused by subject moving and pulsating flow, ghosting artefacts and image stripping. DWI volumes with more than 10% of the weighted images removed, or with a compromised b0 image were excluded.
DWI data were denoised using a joint anisotropic LMMSE filter for Rician Noise.
b0 was extracted and skull-stripped using FSL’s BET tool, and DTI model was fit within the brain mask using an unweighted linear least-squares method.
FA, MD, AD and RD maps were calculated from the resultant tensor image.
The four scalar metrics were co-registered to the T1-w image using FSL’s flirt tool, and then non-linearly registered to the Eve template using DRAMMS for the next step. (These two registrations were done in the end applying a single warp to the scalar DTI maps).
A 3-tissue class T1-w segmentation was performed using FSL’s FAST tool in order to obtain Grey Matter (GM), White Matter (WM) and Cerebrospinal Fluid (CSF) labels. 3-tissue means that signal fractions \(T_{WM}\), \(T_{GM}\) and \(T_{CSP}\) are extracted for each volume unit.

Evidence of the need for harmonization

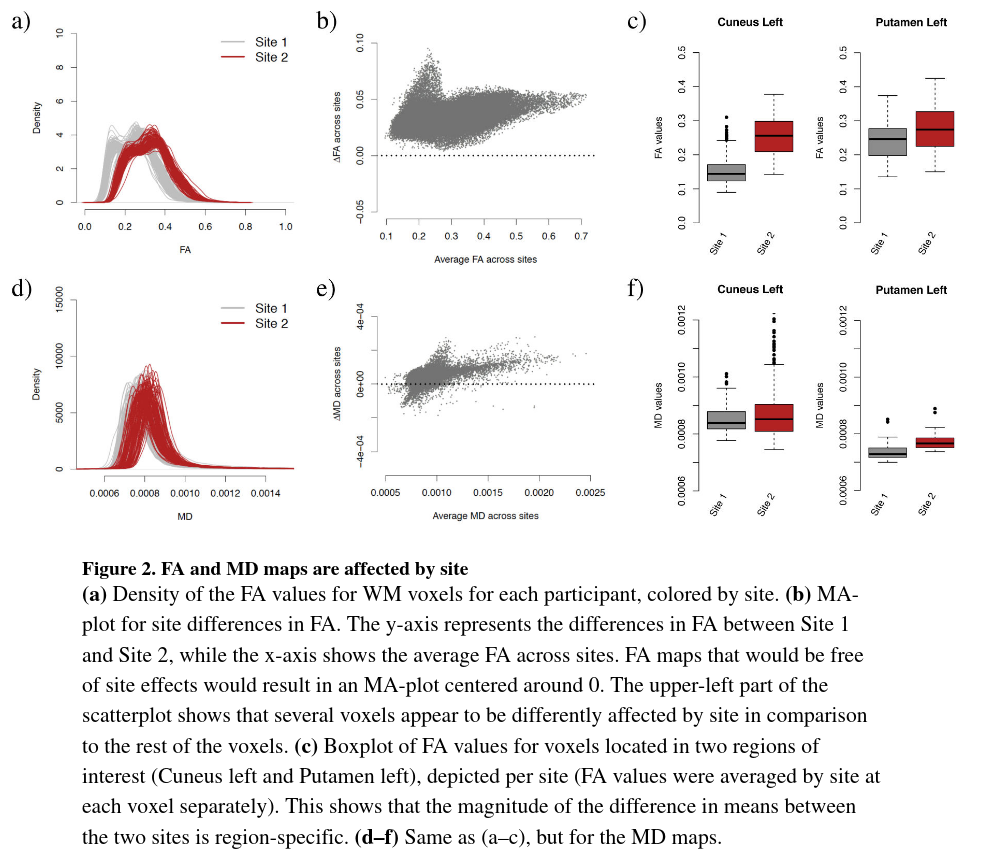
Figure 2a present the histogram of FA values for the WM voxels for each participant statifies by site, see figure A1 for more details about how the curves are obtained. We observe a striking systematic difference between the two sites for all values of FA with an overall difference of 0.07 in the WM (Welch two-sample t-test, p< 2.2e–16).
We can notice the inter-site variability in the histograms is much larger than the intra-variability, confirming the importance of harmonizing the data across sites.
Figure 2b is a MA-plot (or Tukey mean-difference plot or Bland-Altman plot), see figure A2 for more details about its construction with DTI images. It has been used extensively in the genomic litterature to compare treatments and investigate dye bias. It is used here to visualize voxel-wise between-site differences in the FA values plotting the average between-site differences as a function of the average across sites. One can observe that all pixels are globally shifted positively (+0.03) indicating global site differences. Additionally, there is a large proportion of the voxels (top left voxels) that appear to behave differently from other voxels. In the white matter atlas, these voxels are identified as being located in the occipital lobe (middle, inferior and superior gyri, and cuneus), in the fusiform gyrus and in the inferior temporal gyrus. This indicates that the site differences are region-specific, and that a global scaling approach will be most likely insufficient to correct for such local effects.

Figure A1 - Construction of an histogram per voxel position

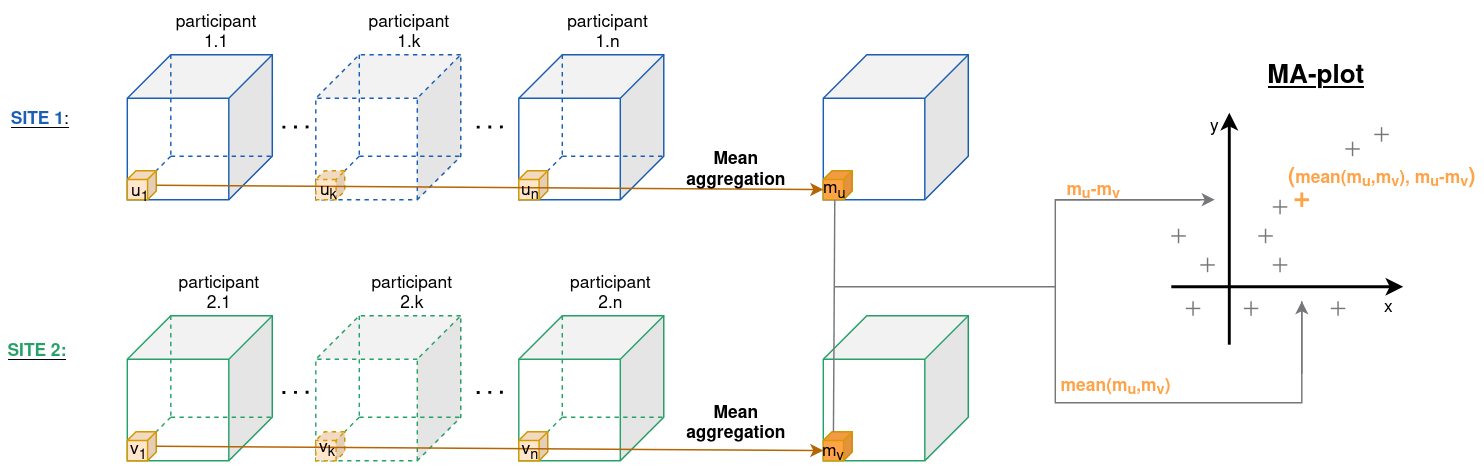
Figure A2 - Construction of a MA plot with DTI data volumes

Harmonisation methods

The authors use and adapt five statistical harmonization techniques for DTI data: global scaling, functional normalization², RAVEL³, Surrogate Variable Analysis (SVA)⁴⁵ and ComBat⁶. Raw data means that no harmonization was performed.

The RAVEL algorithm attempts to estimate a voxel-specific unwanted variation term by using a control region of the brain to estimate latent factors of unwanted variation common to all voxels.

The SVA algorithm estimates latent factors of unwanted variation, called surrogate variables, that are not associated with the biological covariates of interest. It is particularly useful when the site variable is not known, or when there exists residual unwanted variation after the removal of site effects.

ComBat

ComBat model was introduced in the context of gene expression analysis by Johnson et al. [2007] ⁶ as an improvement of location/scale models for studies with small sample size. The ComBat model is reformulated in the context of DTI images. Let \(m\) the number of imaging sites, containing \(n_i\) for \(i=1,2,...,m\) volume scans. For voxel \(\nu=1,2,...,p\), let \(y_{ij\nu}\) represents the diffusion metric measure (FA for e.g.) at voxel \(\nu\) for the scan \(j\) at site \(i\). ComBat posits the following location and scale (L/S) adjustement model:

\[y_{ij\nu} = \alpha_{\nu} + X_{ij}\beta_{\nu} + \gamma_{i\nu} + \delta_{i\nu}\epsilon_{ij\nu} \qquad (1)\]

where \(\alpha_\nu\) is the overall diffusion metric measure for voxel \(\nu\), X is a design matrix for the covariates of interest (e.g. gender, age), and \(\beta_\nu\) is the voxel-specific vector of regression coefficients corresponding to X. One can assume that the error terms \(e_{ij\nu}\) follow a normal distribution with mean zero and variance \(\sigma_\nu^2\). The terms \(y_{i\nu}\) and \(\delta_{iv}\) represent the additive and multiplicative site effects of site \(i\) for voxel \(\nu\) respectively.

One wants to remove these site-effects, preserving the covariates effect. The modelisation can be seen as a simple linear regression at voxel \(\nu\) at site \(i\).

When it is possible to compute \(\gamma_{i\nu}\) and \(\delta_{i\nu}\), the harmonization process is then quite straightforward as the final ComBat-harmonized diffusion metric values would be defined as:

\[y_{ij\nu}^{ComBat} = \frac{y_{ij\nu}-\alpha_{\nu} - X_{ij}\beta_{\nu}-\gamma_{i\nu}}{\delta_{i\nu}} + \alpha_\nu + X_{ij}\beta_\nu \qquad (2)\]

Howether, \(\gamma_{i\nu}\) and \(\delta_{i\nu}\) often have to be estimated. ComBat uses an empirical Bayes (EB) framework to improve the variance of the parameter estimates \(\hat\gamma_{i\nu}\) and \(\hat\delta_{i\nu}\). It estimates an empirical statistical distribution for each of those parameters by assuming that all voxels share the same common distribution. In that sense information from all voxels is used to inform the statistical properties of the site effects. More specifically, the site effects parameters are assumed to have the parametric prior distributions:

\[\gamma_{i\nu}\sim \mathcal{N}(\gamma_i, \tau_i^2) \qquad and \qquad \delta_{i\nu}^2 \sim InverseGamma(\lambda_i,\theta_i) \qquad (3)\]

The hyperparameters \(\gamma_i\), \(\tau_i^2\), \(\lambda_i\), \(\theta_i\) are estimated empirically from the data as described in ⁶. The ComBat estimates \(\gamma_{i\nu}^*\) and \(\delta_{i\nu}^*\) of the site effect parameters are computed using conditional posterior means.

The final ComBat-harmonized diffusion metric values are defined as:

\[y_{ijv}^{ComBat} = \frac{y_{ij\nu}-\hat\alpha_\nu -X_{ij}\hat\beta_\nu - \gamma_{i\nu}^*}{\delta_{i\nu}^*} + \hat\alpha_\nu + X_{ij}\hat\beta_\nu \qquad (4)\]

How does it work in practice ?

Another bibliography session ?

Evaluation framework

A harmonization method is considered to be successful if:

It removes the unwanted variation induced by site, scanner or differences in imaging protocols.
It preserves between-subject biological variability.

NB: both conditions have to be tested at the same time, otherwise it is useless to remove or not the site-effects.

To evaluate (1), the authors calculate two-sample t-tests on the DTI intensities, testing for a difference between Site 1 and Site 2 measurements. They perform the analysis at both voxel and ROI level.

The evaluation of (2) is based on the replicability and validity of voxels associated with biological variation, using age as the biological factor of interest. Replicability is defined as the chance that an independent experiment will produce a similar set of results, and is a strong indication that a set of results is biologically meaningful. Associations with age are measured using usual Wald t-statistics from linear regression. They test the replicability of the voxels associated with age using a discovery-validation scheme.

Creation of silver-standards

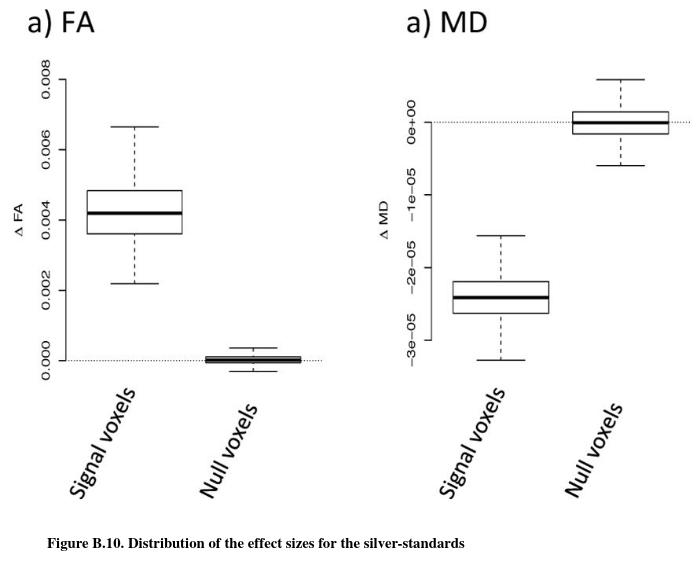
To further evaluate the performance of the different harmonization methods, two sets of silver-standards per site were created:

A silver-standard for voxels that are truly associated with age (signal silver-standard).
A silver-standard for voxels that are not associated with age (null silver-standard).

For each silver-standard two different sets are created since previous studies have shown that some brain regions are more specific in changes for FA and others for MD.

To estimate them, the authors use a meta-analytic approach:

for each site separatly, at each voxel in the WM, they apply a linear regression model to obtain a t-statistic measuring the association of FA with age.
For each site, they define the site-specific signal silver-standard to be the k=5000 voxels with the highest t-statistics in magnitude.
Then, they define the signal-silver standard to be the intersection of the two site specific signal silver-standards.

This process ensures that the resulting voxels are not only voxels highly associated with age within a study, but also replicated across the two sites. Voxels obtained are consistent with the litterature.

Similarly the authors estimate the silver standard for voxels not associated with by age when considering the k=5000 voxels with the lowest t-statistics by site.

Results

DTI scalar maps are highly affected by site

See figure 2

ComBat successfully removes site effects in DTI scalar maps

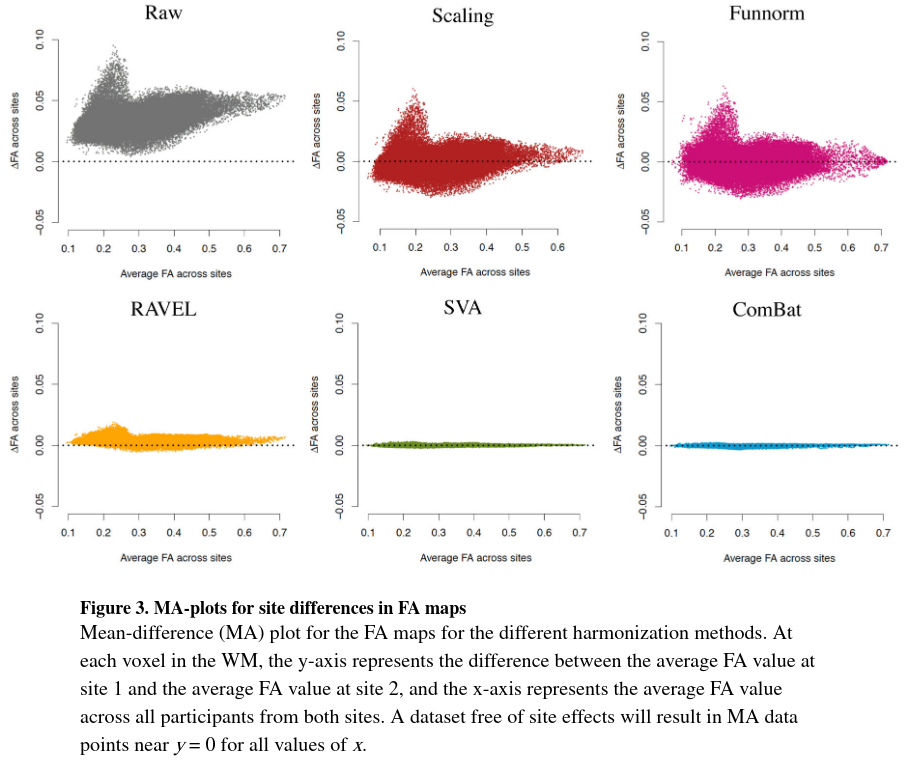
Figure 3 shows the MA-plots before and after each harmonization for the FA maps.

Scaling and Funnorm methods centered the MA-plots around 0, which is consistent with the global nature of their harmonization methods.
RAVEL, SVA and ComBat reduce greatly the inter-sites differences.
Ravel does not seem to account for local-site effects.

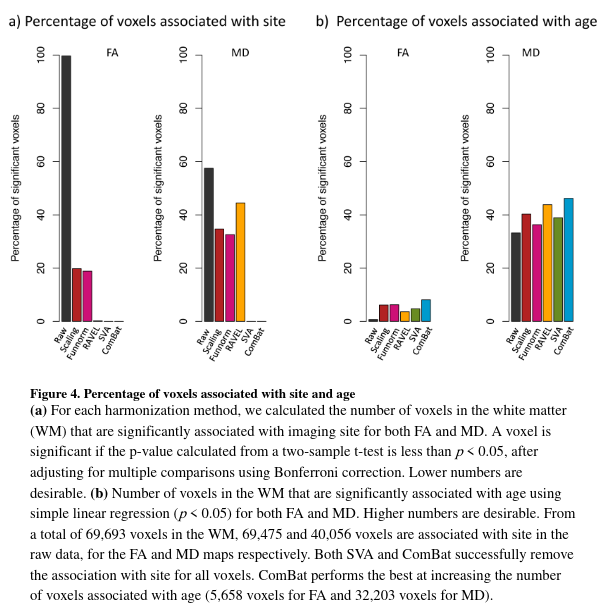
Figure 4a shows a t-statistic at each voxel to measure the association of the DTI scalar values with site. A voxel is significant if the p-value calculated from the two-sample t-test is less than 0.05, after correcting for multiple comparisons using Bonferroni correction. The authors do not explain how they realize the correction in practice. For more details about how they perform a two-sample t-statistics with DTI data, see Figure A.3.

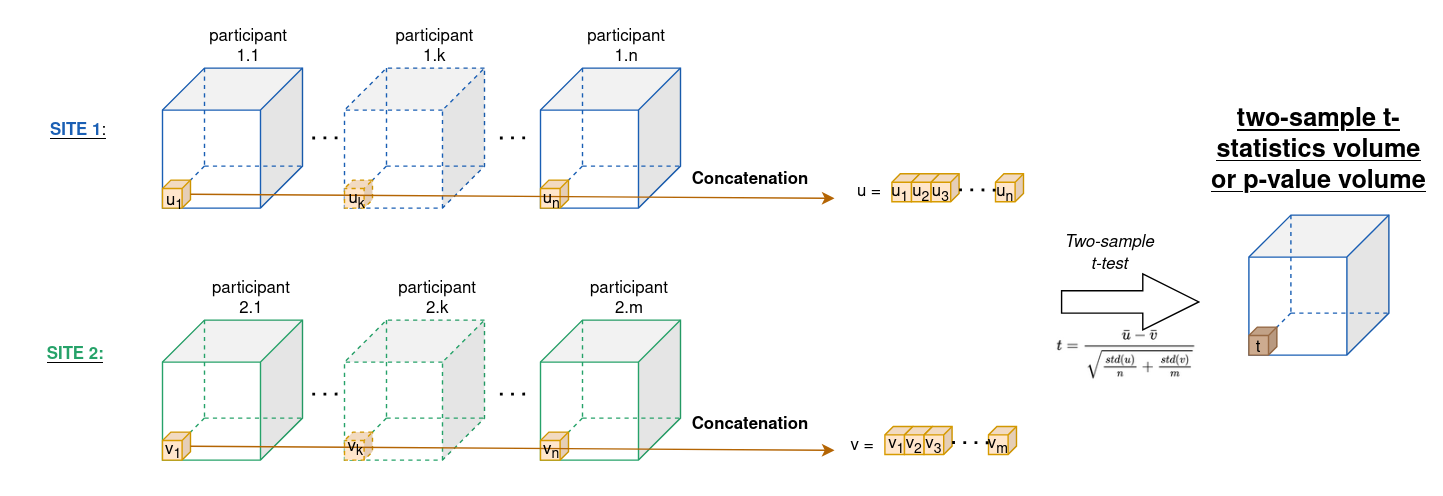
Figure A3 - Process for computing two-sample t-statistics / p-values on two databases from Site 1 and Site 2 at voxel level. This helps to calculate the percentage of voxels associated with site.

Most voxels are associated with site in the absence of harmonization (raw data). And all harmonization methods reduce the number of voxels associated with site for both FA and MD maps at different degree.

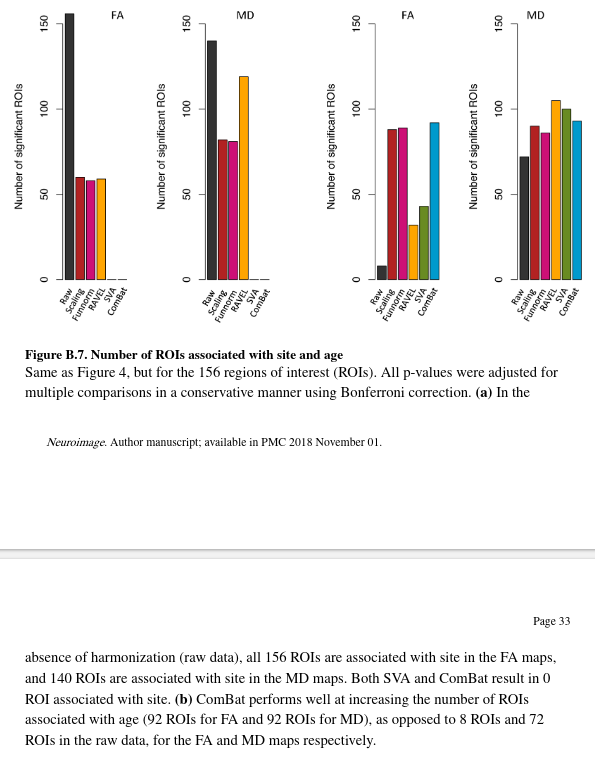
The authors also calculated t-statistics after summarizing FA and MD values by brain region. Using the Eve template atlas, they identified 156 region of interests (ROIs) overlapping with the WM mask.

In the absence of harmonization, all ROIs are associated with site.
ComBat and SVA fully remove site effects for all ROIs.

Harmonization across sites preserves within-site biological variability

For each site, the authors computed t-statistics for association with age before and after harmonization, see figure A4 for more details. Then, for a given site, they compute the Spearman correlation between the unharmonized t-statistics and the harmonized statistics. The idea is that voxels that were clearly associated with age before harmonization should remain so.

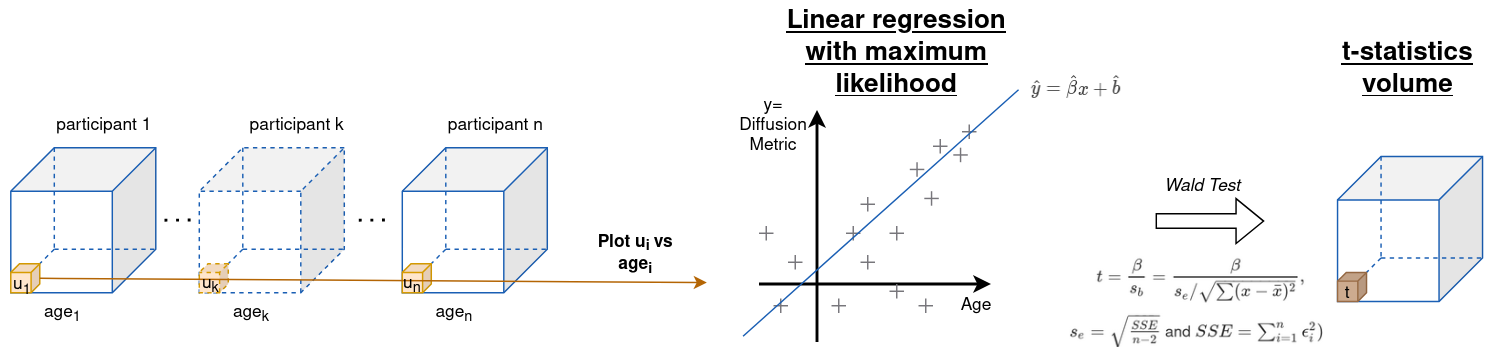
Figure A4 - Computation of a p-statistic per voxel position. All participant provide as data their DTI volume and their age at the time of acquisition..

The authors obtained the following Spearman correlations:

	Scaling	Funorm	RAVEL	SVA	ComBat
Spearman correlation	0.997	0.997	0.981	0.893	0.994

All harmonization methods seem to preserve within-site biological variability, except SVA which has a substantially lower correlation than the other methods. This is not suprising according to the authors because SVA removes variability that is not associated with age across the whole dataset but does not protect for the removal of biological variability at each site individually.

Additionally, as we can see in Figure 4b, all harmonization methods increase the number of significant voxels associated with age in comparison to the raw data (ComBat presents the highest gain for both FA and MD maps).

Harmonization and confounding

This part aims to investigate the robustness of the different harmonization techniques to datasets for which age is confounded by site.

The two main datasets are carefully matched for age, gender, ethnicity to minimize potential confounding of those kind of variables with site. Howether matching has limitations as it strongly depends on the overlap of covariates between datasets. Poor overlap means many scans to be excluded, making matching infeasible in many applications where harmonization is needed.
Howether, doing nothing will allow an undesirable situation to arise in which the site is a confounding factor for the relationship between the DTI values and the phenotypes of interest.
Confounding between age and site presents an additional challenge for harmonization, since removing variation associated with site can lead to removing variation associated with age if not done carefully.

To evaluate the robustness of the different harmonization methods in the presences of statistical confounding between imaging site and age (that is when age is unbalanced with respect to site), the authors selected different subsets of the data to create confounding scenarios.

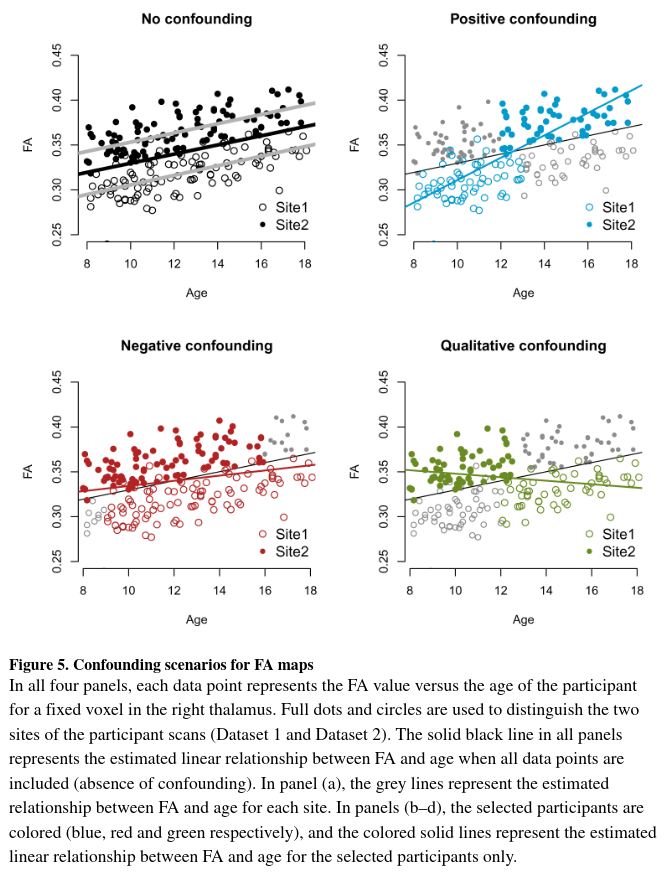
For illustration purpose, Figure 5 shows only one voxel in the right thalamus for which the association between FA and age is high.
They observe that for the full data (Figure 5a), the FA values increase linarly with age within site.
“Positive confounding” and “negative confounding” refer to situations where the relationship between the FA values and age is overestimated and underestimated, respectively, with the same directionality of the true effect.
The no-confounding scenario of Figure 5a shows the association of the FA values with age is unbiased in the sense that it is not modified by site. Indeed, the slope using all the data (black line) is similar to the slopes estimated within each site (grey lines). However, the variance of the estimated slope will be inflated due to the unaccounted variation attributable to site.

ComBat improves the replicability of the voxels associated with age

They evaluate replicability which is defined as the chance that an independent experiment will produce a similar set of results and is a strong indication that a set of results is biologically meaningful.

They test the replicability of voxels associated with age following a discovery-validation scheme. (See section 2.4 of the paper).

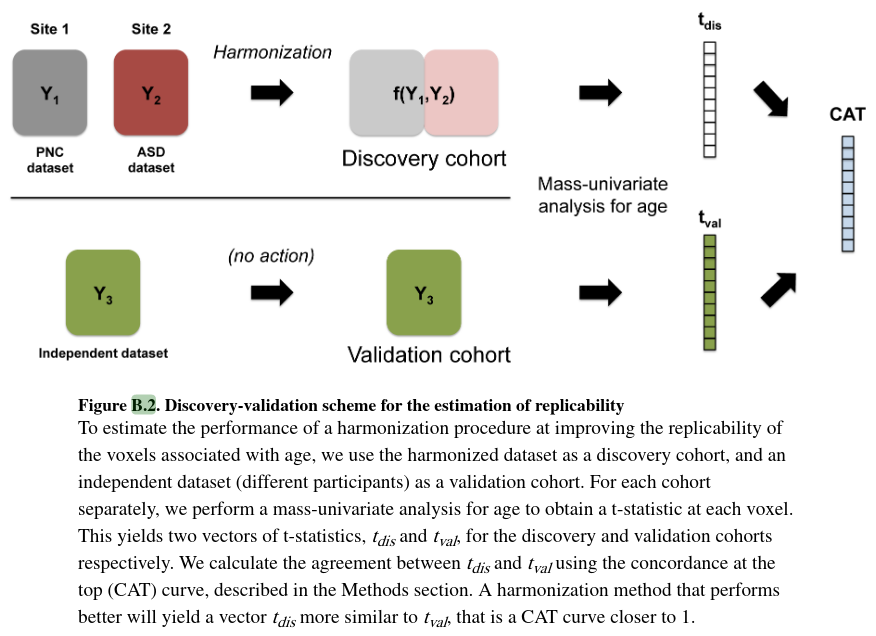
They consider the harmonized dataset as a discovery cohort and two independent datasets as validation cohorts.
They peform a mass-univariate analysis testing for association with age separatly for each cohort.
They use Concordance At Top (CAT) curves to measure the replicability of the results between the discovery and validation cohorts.

This evaluates the performance of the different harmonization methods at replicating the voxels associated with age across independent datasets.

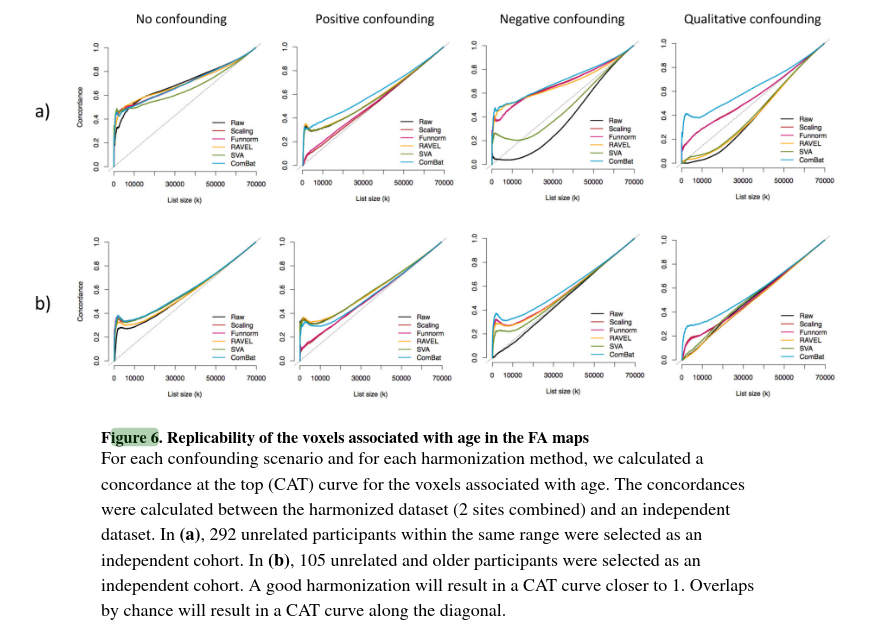
In Figure 6a, CAT curves using Independent Dataset 1 as a validation cohort (same age range) are plotted:

No confounding case: all methods including raw data performs well. ComBat performs best with a flat CAT curve around 1.
Positive confounding: Similar performance to the raw data except for the scaling and Funnorm methods. This is not suprising because both approach are global approaches, and because of the nature of the confounding, the removal of a global shift associated with site will also remove the global signal associated with age.
Negative and qualitative confounding: combining the data without a proper harmonization technique lead to more severe problems. The raw data curve is far below the diagonal line, indicating a negative correlation. The authors explain that due to these confounding, the t-statistics for each voxel that are truly not associated with age, normally centered around 0, became highly negative because of the site effect. On the other hand, t-statistics for the voxels associated with age are shifted towards 0. These confoundings render the null voxels significant and create a reversed ranking.

These experiences, added to the experiences in figure 6b., show that ComBat is a robust harmonization method when the other methods show variable performance.

ComBat successfully recovers the true effect sizes

In this section, the authors evaluate the bias in the estimated changes in FA associated with age (\(\hat\Delta_{age}FA\)) for each harmonization procedure, for the different confounding scenarios. They refer to \(\hat\Delta_{age}FA(\nu)\) as the estimated “effect size” for voxel \(\nu\). The “effect size” can be estimated using linear regression (slope coefficient associated with age) for each voxel. To assess unbiasedness without knowing the true effect sizes, the authors curcumvent by estimating the effect sizes on the signal silver-standard (in practice, they compute for each voxel the mean of the slopes they obtain for each site in the silver-standard).

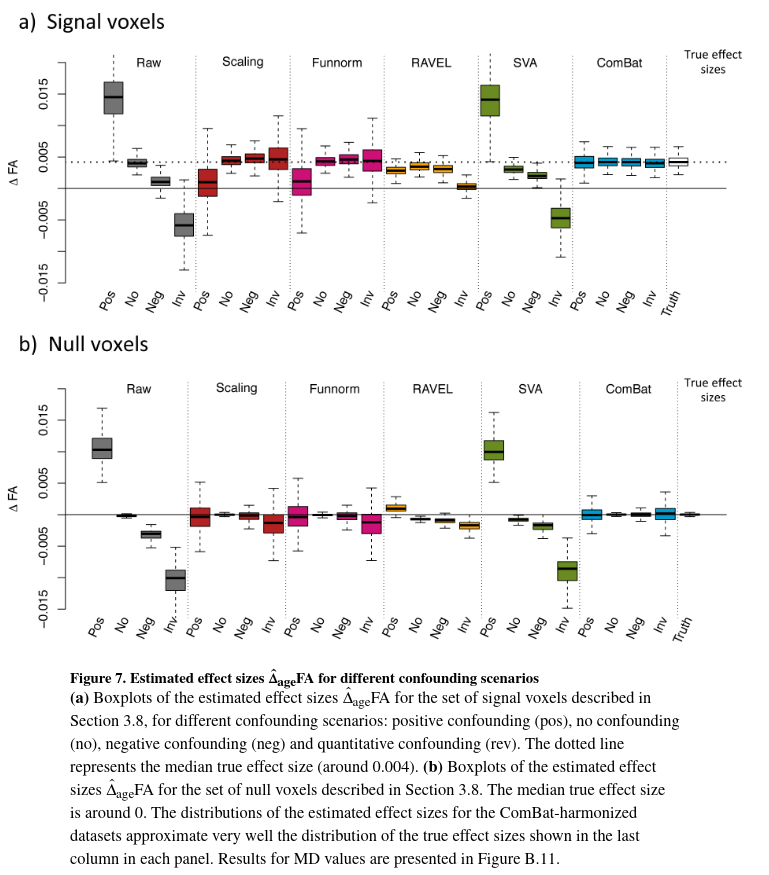
Figure B.10a shows the boxplots of the "effect sizes" from their silvert-standard. In these cohorts, a difference is made between signal voxels and null voxels.

Figure 7 presents the distribution of the estimated effect sizes on the signal silver-standard for all methods and for all confounding scenarios. The dashed line represents the median of the true effect sizes, and the solid line represents an effect size of 0.

Results for raw data are consistent: positive (resp. negative) confounding shifts the effect size positively (resp negatively). ComBat is the only harmonization technique that fully recovers the true effect sizes for all confounding scenarios in terms of median value and variability.

ComBat improves statistical power

Figure 8 show the distribution of the WM voxels-wise t-statistics measuring association with age in the FA maps for four combinations of the data: site 1 and site 2 analysed separately, Site 1 and Site 2 combined without harmonization and harmonized with ComBat.

The distribution of the t-statistics for the two sites combined without harmonization is shifted towards 0 in comparison to the t-statistics obtained from both sites separately. This strongly indicates that combining data from multiple sites, without harmonization, is counter-productive and impairs the quality of the data.
Combining and harmonizing data with ComBat results in a distribution of higher t-statistics on average.
Same observations with the silver-standards of site 1 and 2 (Figure 8.c and 8.d).

ComBat is robust to small sample size

A major advantage of ComBat over other methods is the use of Empirical Bayes to improve the estimation and removal of the site effects in small sample size settings. To assess the robustness of the different harmonization approaches for combining small samples size studies, the authors created B = 100 random subsets of size n = 20 across sites (10 from site 1 and 10 from site 2.). After applying the different harmonization methods, they calculated voxel-wise t-statistics in the WM for testing the association of the FA with age, for a total of 100 t-statistic maps.

To obtain a silver-standard, they created B = 100 random subsets of size 20 with only patients from Site 1 and a B=100 again with patients from Site 2. Because subsets are created within site, they are not affected by site effects and results obtained from those subsets should be superior or as good as any of the results obtained from the harmonized subsets.

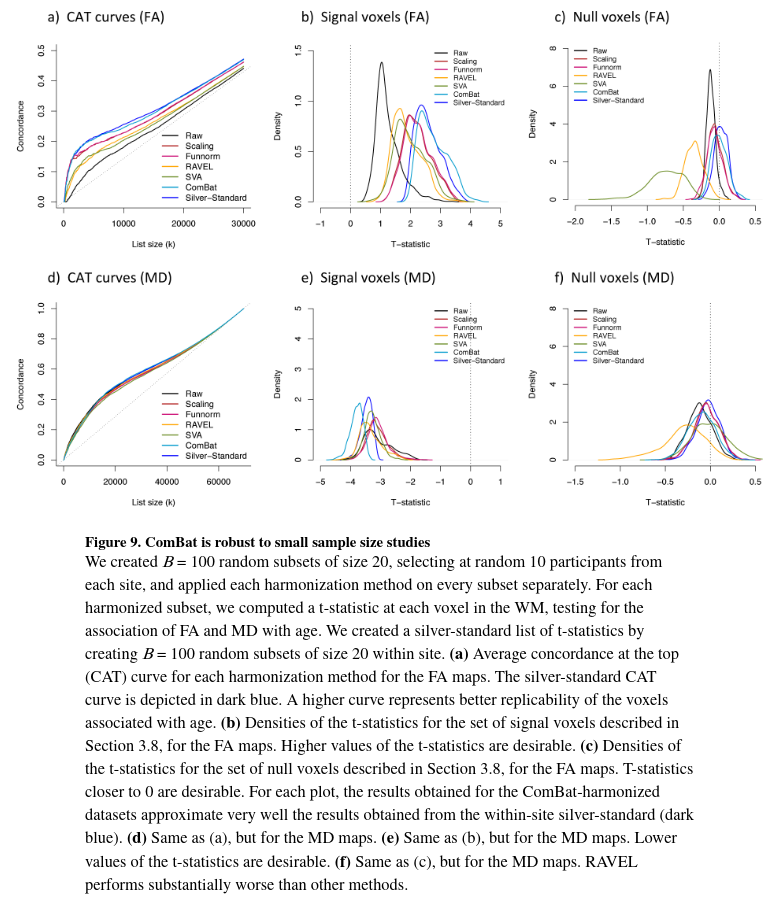
Figure 9a shows the average CAT curve for each harmonization method (average taken across the random subsets) together with the silver-standard CAT curve (dark blue) for the FA maps.

All methods improve the replicability of the voxels associated with age.
ComBat performs as well as the silver-standard, successfully removing most of the site effects.

Figure 9.b shows the densities of the t-statistics for the top voxels associated with age (signal voxels) for the FA maps.

All methods improve the magnitude of the t-statistics, therefore increasing statistical power, with ComBat showing the best performance as well as the silver-standards.

Figure 9.c shows the densities of the t-statistics for the voxels not associated with age (null voxels) for the FA maps.

A good harmonization method should result in t-statistics centered around 0.
Performance is variable across harmonization methods. But ComBat is one of those who do perform correctly.

The authors investigated the stability of the ComBat harmonization parameters by running ComBat on random subsamples of variable size. They obtained that site effects estimated from subsamples approximate well the site effects estimated from the full dataset.

Discussion

The authors shows that combining the two studies without proper harmonization led to a decrease in power of detecting voxels associated with age.
This confirmed that DTI measurements are highly affected by small changes in the scanner parameters, as those affect the underlying water diffusitivity.
Similar results were obtained from MD maps.
ComBat allows site effects to be location-specific, but pools information across voxels to improve the statistical estimation of the site effects.
ComBat substantially increases the replicability of the voxels associated with age across independent experiments.
ComBat is the best harmonization method in this study at improving the result across all confounding scenarios between age and site.
ComBat is a very promising harmonization method even for small sample size studies, doing as well as a dataset that was not affected by site effects.
Other methods didn’t perform well overall. Some fail to account for the spatial heterogeneity of the site effects thoughout the brain (global Scaling and functional normalization). Others failed on other diffusion metrics (RAVEL on MD maps). And others failed to not confound age and site-effects on the diffusion metrucs (SVA).
Finally the ComBat model does not make any assumptions regarding the neuroimaging techniques. ComBat algorithm can be applied at voxel level, but also at ROI level.

Limitations ?

To be continued …

References

(Alexander, Andrew L., Lee, Jee Eun, Lazar, Mariana, Field, Aaron S. Diffusion tensor imaging of the brain. Neurotherapeutics. 2007; 4(3):316–329. [PubMed: 17599699]) ↩
Fortin, Jean-Philippe, Labbe, Aurelie, Lemire, Mathieu, Zanke, Brent, Hudson, Thomas, Fertig, Elana, Greenwood, Celia, Hansen, Kasper D. Functional normalization of 450k methylation array data improves replication in large cancer studies. Genome Biology. 2014; 15(11):503.doi: 10.1186/ s13059-014-0503-2 [PubMed: 25599564] ↩
Fortin, Jean-Philippe, Sweeney, Elizabeth M., Muschelli, John, Crainiceanu, Ciprian M., Shinohara, Russell T. Alzheimer’s Disease Neuroimaging Initiative, et al. Removing inter-subject technical variability in magnetic resonance imaging studies. NeuroImage. 2016a; 132:198–212. [PubMed: 26923370] ↩
Leek, Jeffrey T., Storey, John D. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genetics. 2007; 3(9):1724–1735. DOI: 10.1371/journal.pgen.0030161 [PubMed: 17907809] ↩
Leek, Jeffrey T., Storey, John D. A general framework for multiple testing dependence. Proceedings of the National Academy of Sciences. 2008; 105(48):18718–18723. DOI: 10.1073/pnas.0808709105 ↩
Evan Johnson W, Li Cheng, Rabinovic Ariel. Adjusting batch effects in microarray expression data using empirical bayes methods. Biostatistics. 2007; 8(1):118–127. [PubMed: 16632515] ↩ ↩² ↩³