Adding Conditional Control to Text-to-Image Diffusion Models
Highlights
- ControlNet is a method to spatially condition text-to-image Diffusion or Latent Diffusion models.
- Used a lot in different context (even in the medical field).
- The method is not complex and is already implemented on MONAI here
Introduction
Diffusion models can create visually stunning images by typing in a text prompt, but they are limited in the control they provide over the spatial composition of the image. In particular, it is difficult to accurately express complex layouts and poses using text prompts alone.
ControlNet is a neural network architecture that can add spatial control (e.g. edge maps, human pose skeletons, segmentation maps, depth, normals, etc.) to large pre-trained text-to-image diffusion models.
Methods
ControlNet is a neural network architecture designed to add more spatial control while maintaining the quality and robustness of a large pretrained model (specifically in the case of the text-to-image model from Stable Diffusion model [1]).
To achieve this, the parameters of the original model are locked while a trainable copy of the encoding layers is created, leveraging Stable Diffusion as a strong backbone. The trainable copy is connected to the original locked model through zero convolution layers, where the weights are initialized to zero and gradually adapt during training. This design prevents the introduction of disruptive noise into the deep features of the diffusion model at the early training stages, thereby preserving the integrity of the pretrained backbone in the trainable copy.
They demonstrate that ControlNet effectively conditions Stable Diffusion using various input modalities, including Canny edges, Hough lines, user scribbles, human key points, segmentation maps, shape normals, and depth information.
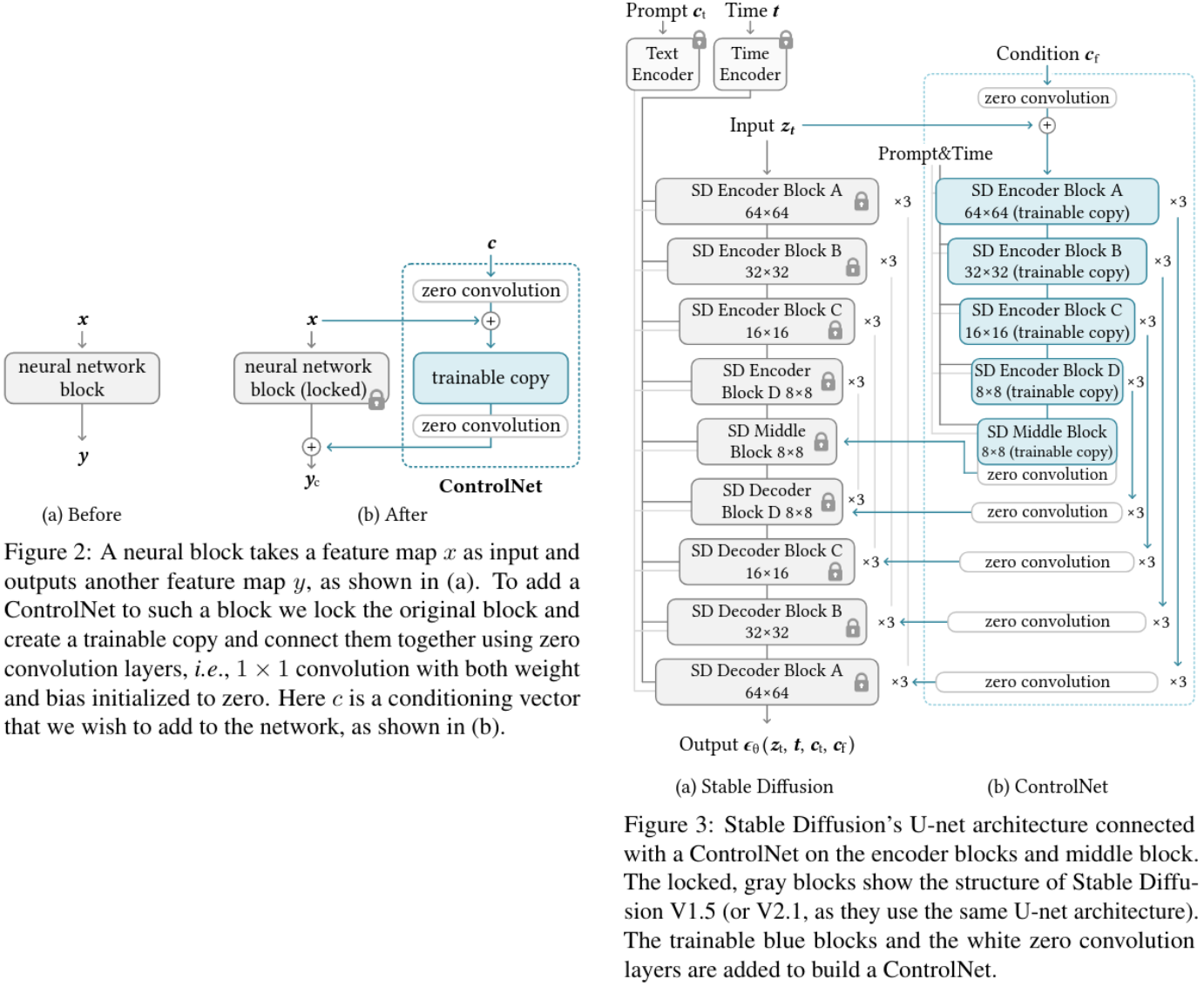
The complete ControlNet then computes (Fig. 2b):
\[y_c = \mathcal{F}(x; \Theta) + \mathcal{Z} \big( \mathcal{F} \big(x + \mathcal{Z}(c; \Theta_{z1}); \Theta_c \big); \Theta_{z2} \big)\]- \(\mathcal{Z}(.;.)\) is a \(1 \times 1\) convolution layer with both weights and biases initialized to zeros.
- \(\Theta_{z1}\) and \(\Theta_{z2}\) are the parameters of the first and second zero convolution layer.
The objective function aims to minimize the original noise with the estimated noise by computing:
\[\mathcal{L} = \mathbb{E}_{z_0, t, c_t, c_f, \epsilon \sim \mathcal{N}(0,1)} \left[ \left\| \epsilon - \epsilon_{\theta} (z_t, t, c_t, c_f) \right\|_2^2 \right]\]- \(\mathbb{E}_{z_0, t, c_t, c_f, \epsilon \sim \mathcal{N}(0,1)}\) is the average over the distributions of the involved variables
- \(\epsilon\) is the real noise sampled from a standard normal distribution
- \(\epsilon_{\theta}\) is the noise predicted by the neural network, parameterized by \(\theta\)
- \(z_t\) is the feature map \(z\) at timestep \(t\)
- \(t\) is the timestep
- \(c_t\) is the text prompt conditioning
- \(c_f\) is the ControlNet conditioning
Results
CFG Resolution Weighting and Composition

Classifier-free guidance was used in Stable Diffusion model to generate high quality images. To generate these high quality images, they predicted a noise from a conditional and unconditional noise and add them using the formula below:
\[\epsilon_{\text{prd}} = \epsilon_{\text{uc}} + \beta_{\text{cfg}} (\epsilon_c - \epsilon_{\text{uc}})\]- \(\epsilon_{\text{prd}}\) is the model’s final output.
- \(\epsilon_{\text{uc}}\) is the unconditional output.
- \(\epsilon_c\) is the conditional output.
- \(\beta_{\text{cfg}}\) is user-specified weight.
They changed the original CFG (as shown in figure 5) by adding the conditioning image to \(\epsilon_c\) and multiply a weight \(w_i\) (based on the resolution of each block) to each connection between Stable Diffusion and ControlNet.
\(w_i = 64/h_i\) where \(h_i\) is the \(i^{th}\) block. (\(h_1 = 8\), \(h_2 = 16\) …)
By doing so, they reduced the guidance of the conditioning that is too strong and called their approch: CFG Resolution Weighting.
Examples of spatial conditioning and Quantitative results
Examples:

Quantitative results:

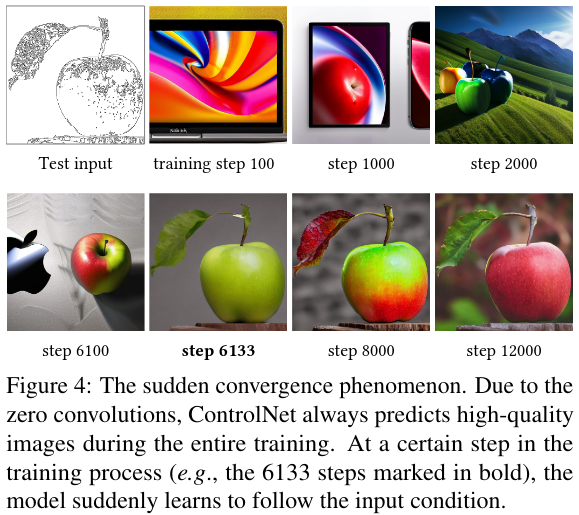
Dataset size and Input interpretation
The impact of the dataset size as well as an example of the network to interpret the content of an input conditioning with low context:

Conclusion
ControlNet is a neural network framework designed to facilitate conditional control in large pre-trained text-to-image diffusion models. It integrates the pre-trained layers of these models to construct a high-capacity encoder for learning specific conditioning signals, while employing “zero convolution” layers to mitigate noise propagation during training.
Empirical evaluations confirm its effectiveness in modulating Stable Diffusion under different conditioning scenarios, both with and without textual prompts. The model proposed by the authors is likely to be applicable to a wider range of conditions, and facilitate relevant applications.