Highlights

Most semantic segmentation networks rely on learning one prototype per class. This approach suffers from several limitations, in particular the lack of representativeness for intra-class variance and the ignorance of intra-class compactness.
The authors propose a segmentation framework, dubbed ProtoSeg, with non-learnable prototypes which adresses these limitations.
The code associated with the paper is available on the official GitHub repository.

Motivation

Most deep learning based semantic segmentation networks (UNet, DeepLab, Swin, etc.) proceed as follow : 1) a learnable encoder \(\phi\) extract dense visual features and 2) a classifier \(\rho\) (also called projection head) that projects pixel features into the label space. Typically, if the task is C-class segmentation, the network ends with a 1x1 convolution layer parametrized by \({\boldsymbol W} = [ {\boldsymbol w_1}, ..., {\boldsymbol w_C} ]^T \in \mathbb{R}^{D \times C}\) where \(D\) is the dimension of the pixel embedding at the last layer of the network (before the projection). The probability of each class for the pixel \(i \in \mathbb{R}^D\) is derived after application of a softmax operation :

\[p(c | i) = \frac{\exp{({\boldsymbol w_c} i)}}{\sum_{c' = 1}^{C}\exp{({\boldsymbol w_{c'}} i)}}\]

In the formalism, each projection vector \({\boldsymbol w_{c}}\) can be seen as a learnable prototype for class c. The idea is the same for transformer-based network which perform parametric pixel-query with learnable query vectors representing each class.

The authors argue that this approach suffers from three main limitations:

Each class is usually only represented by a single prototype per class, which may be insufficient to describe rich intra-class variance.
At least \(D \times C\) parameters are needed for prototype learning, which can hurt generability in the large-vocabuary case.
With cross-entropy loss, only the relative distance between intra-class and inter-class distances are optimized. The actual distance between pixels and prototypes, i.e. intra-class compactness is ignored.

The authors propose to overcome these limitations with a new segmentation framework with non-learnable prototypes (Figure 1).

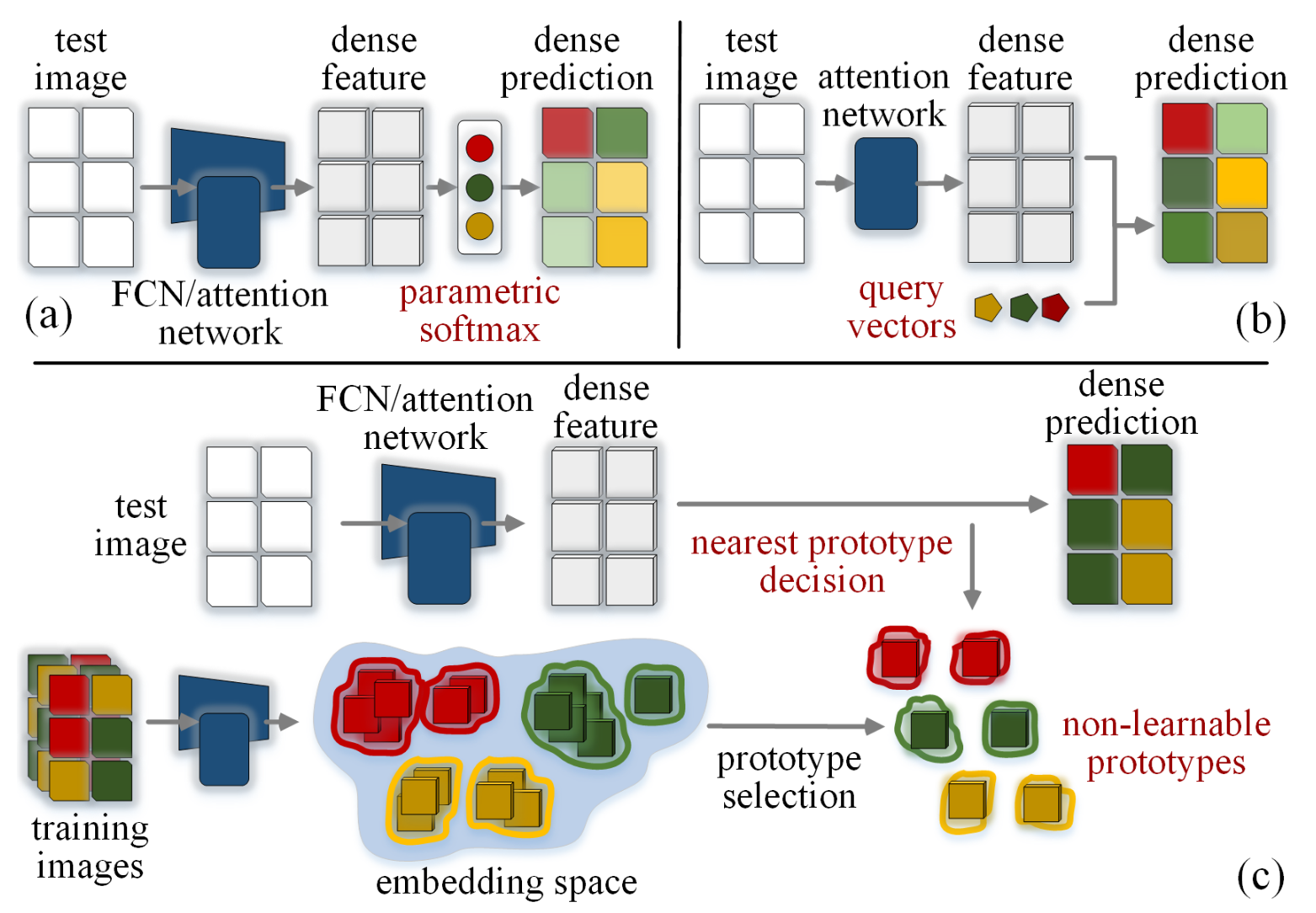
Figure 1. Different semantic segmentation paradigms. (a) Parametric softmax or (b) query vectors for mask decoding, can be viewed as learnable prototype based methods that learn class-wise prototypes in a fully parametric manner. (c) is a nonparametric scheme that directly selects subcluster centers of embedded pixels as prototypes, and achieves per-pixel prediction via nonparametric nearest prototype retrieving.

Non-learnable prototype based semantic segmentation

Let’s consider a encoder network (FCN or attention-based) \(\phi\) which maps an input image \(I \in \mathcal{R}^{h \times w \times 3}\) to a feature tensor \(\boldsymbol{I} \in \mathbb{R}^{H \times W \times D}\). The goal is to perform multi-class semantic segmentation, i.e. pixel-wise \(C\)-class classification.

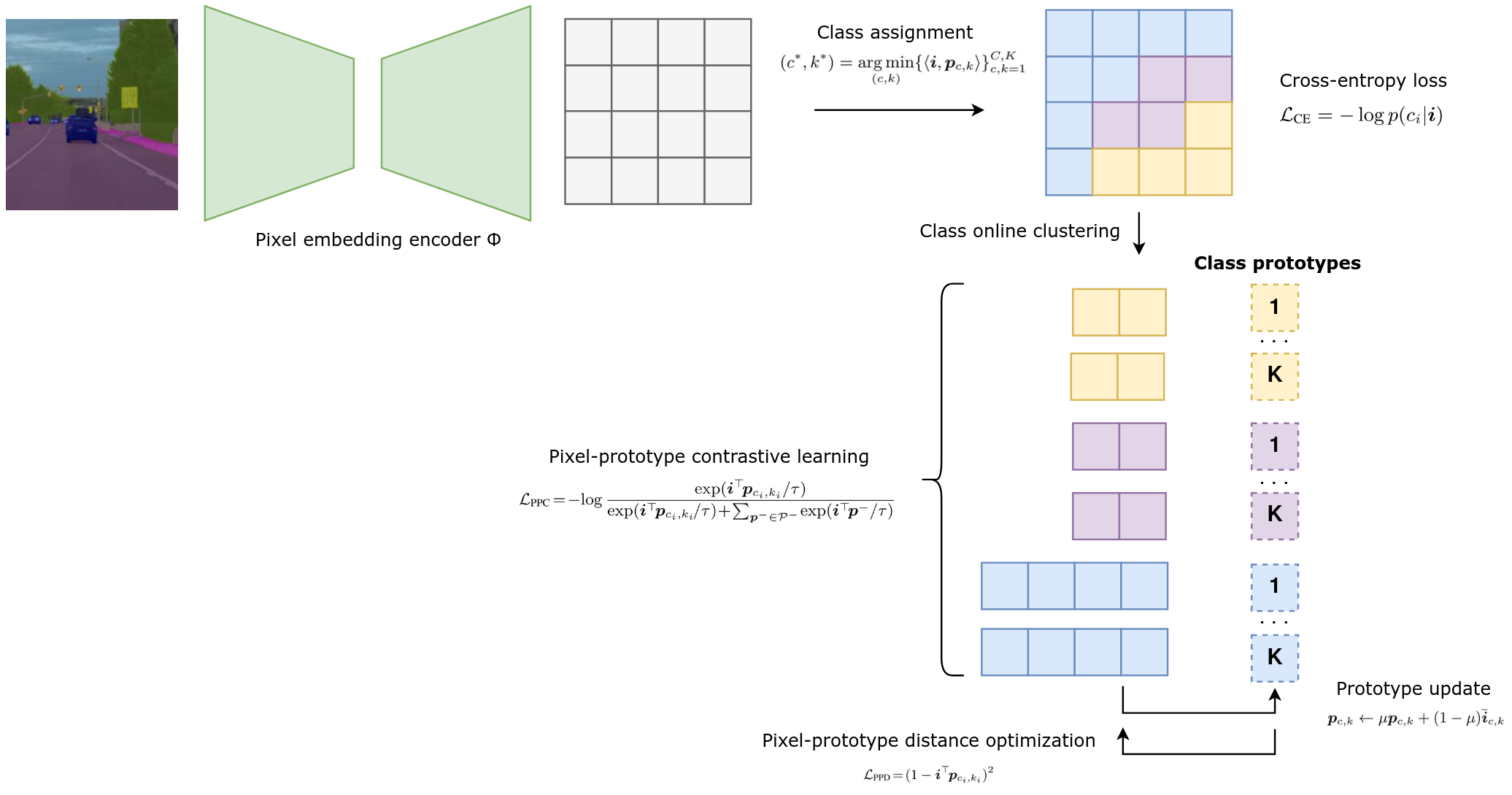
Figure 2. Training procedure of proposed segmentation framework.

First idea. Each class \(c \in \{ 1, ..., C \}\) is represented by a total of \(K\) prototypes \(\{ p_{c,k} \}_{k=1}^K\). A prototype \(p_{c,k}\) is defined as the center (in the pixel embedding space) of the \(k\)-th sub-cluster of training pixel samples belonging to class \(c\). The class \(c^*\) to which a pixel \(i\) is assigned is simply that for which one of the prototypes minimizes similarity with the pixel’s embeddings:

\[(c^*, k^*) = \underset{(c,k)} {\arg \min} \, \{ \langle p_{c,k},i \rangle \}_{c,k=1}^{C,K}\]

where \(\langle \cdot,\cdot \rangle\) is a distance measure between features, for instance negative cosine similarity \(- \langle p,i \rangle = p^T i\). The probability distribution over the \(C\) classes can be computed applying a softmax operation and standard cross-entropy can bu used for training.

However, this idea only comes down to pushing pixel \(i\) to the nearest prototype. It does not address the challenges mentioned above. For instance, if pixel \(i\) embedding matches with a pattern of a certain prototype of class \(c\) but is distant from other prototypes of this class, this dynamic can not be captured here.

Within class online clustering and pixel-protype contrastive learning. The idea is to distribute equally the pixels assigned to a class \(c\) to all its prototypes. More specifically, given pixels \(\mathcal{I}^c = \{ i_n \}_n ^N\) in a training batch that belong to class c, the goal is to map the pixels \(\mathcal{I}^c\) to the \(K\) prototypes of class c with equipartition constraint. This can be efficently done with few iterations of Sinkhorn-Knopp algorithm.

Once a pixel \(i\) is assigned to a class prototype \(p_{c_i,k_i}\), a contrastive loss between prototypes is applied. It forces each pixel embedding \(i\) to be similar with its assigned prototype and dissimilar with other \(CK - 1\) prototypes.

\[\mathcal{L}_{PPC} = - \log \frac{\exp (i^T p_{c_i, k_i} / \tau)}{\sum_{c,k=1}^{C,K} \exp (i^T p_{c, k} / \tau)}\]

Pixel-prototype distance optimization. One limitation mentioned ealier that has not been addressed yet is the compactness of pixel features assigned to the same prototype. The authors propose a compactness-aware loss to further regularize the pixel representations. It aims to minizimze the intra-cluster variability around each prototype.

\[\mathcal{L}_{PPD} = (1 - i^T p_{c_i,k_i})^2\]

Network learning and prototype update. The pixel embedding space \(\phi\) is learnt by stochastic gradient descent based on a combination of the three losses mentioned above:

\[\mathcal{L}_{tot} = \mathcal{L}_{CE} + \lambda_1 \mathcal{L}_{PPC} + \lambda_2 \mathcal{L}_{PPD}\]

The non-learnable prototypes \(\{ p_{c,k}\}_{c,k=1}^{C,K}\) are updated via exponential moving average as follows:

\[p_{c,k} \leftarrow \mu p_{c,k} + (1 - \mu) \overline{i}_{c,k}\]

where \(\mu \in [0,1]\) is the momentum parameter and \(\overline{i}_{c,k}\) is the mean embedding vector of all the pixels which have been assigned to prototype \(p_{c,k}\)

Results

The two tables below show some quantitative segmentation results on the datasets ADE-20k and Cityscapes, and examples of segmentations are displayed on Figure 5.

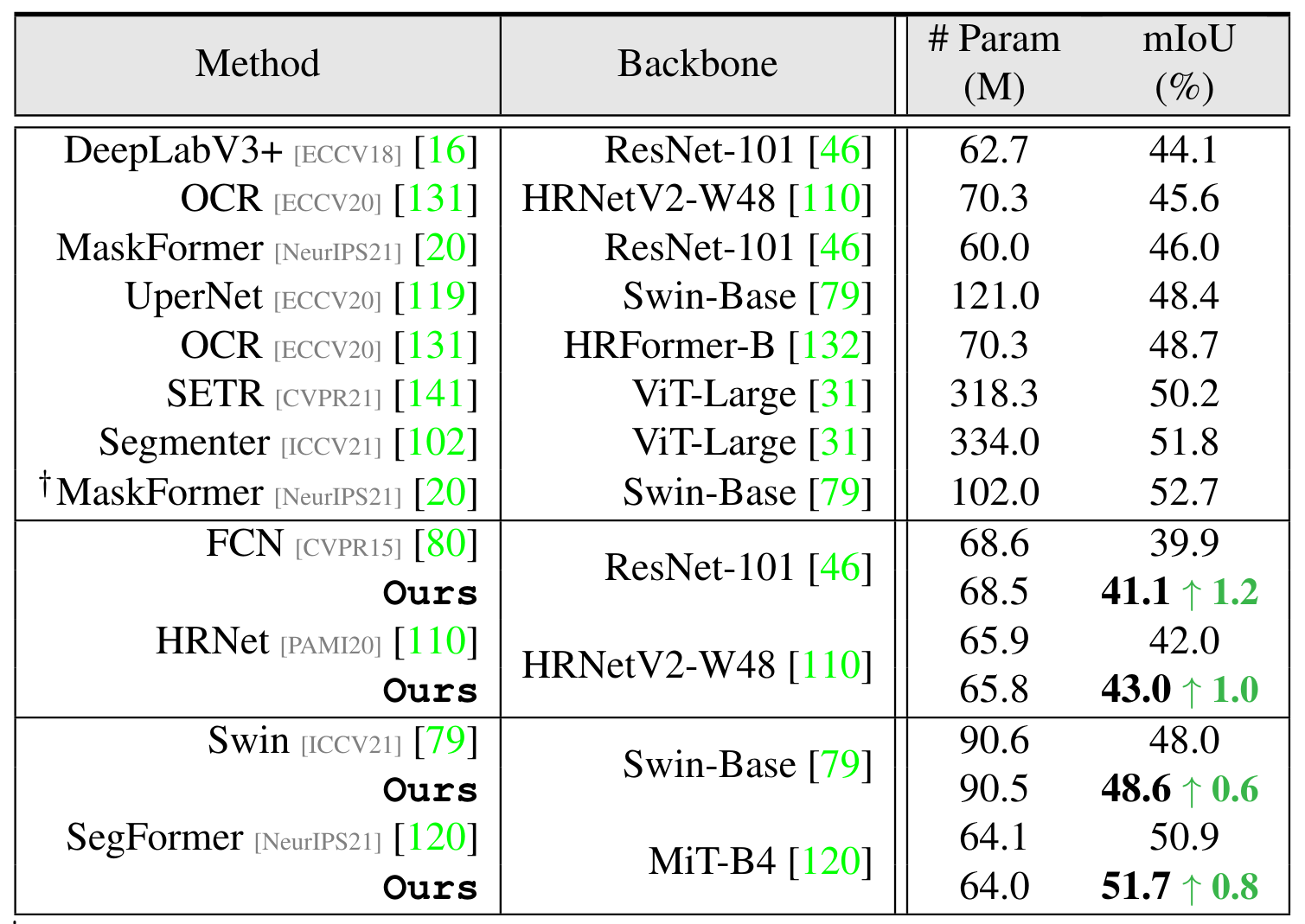
Figure 3. Quantitative results on ADE-20K.

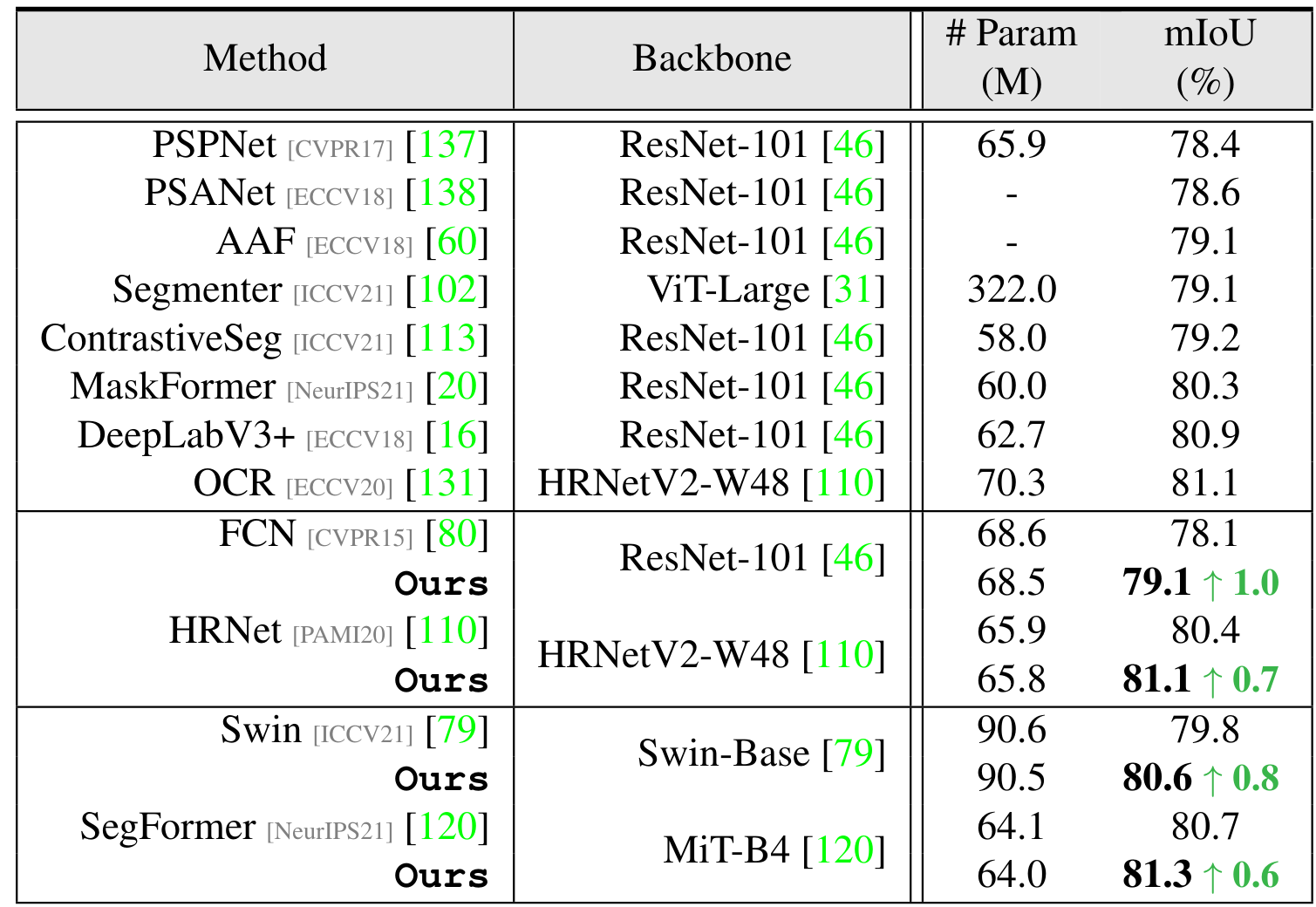
Figure 4. Quantitative results on Cityscapes.

Figure 5. Examples of segmentations.

The figures below provide two visualizations of the effectiveness of prototype learning for semantic segmentation.

Figure 6. Visualization of pixel-prototype similarities for classes person (top) and car (bottom). The model has been trained with three prototypes per class and the similarity with each prototype is encoded by a color channel (red, blue or green).

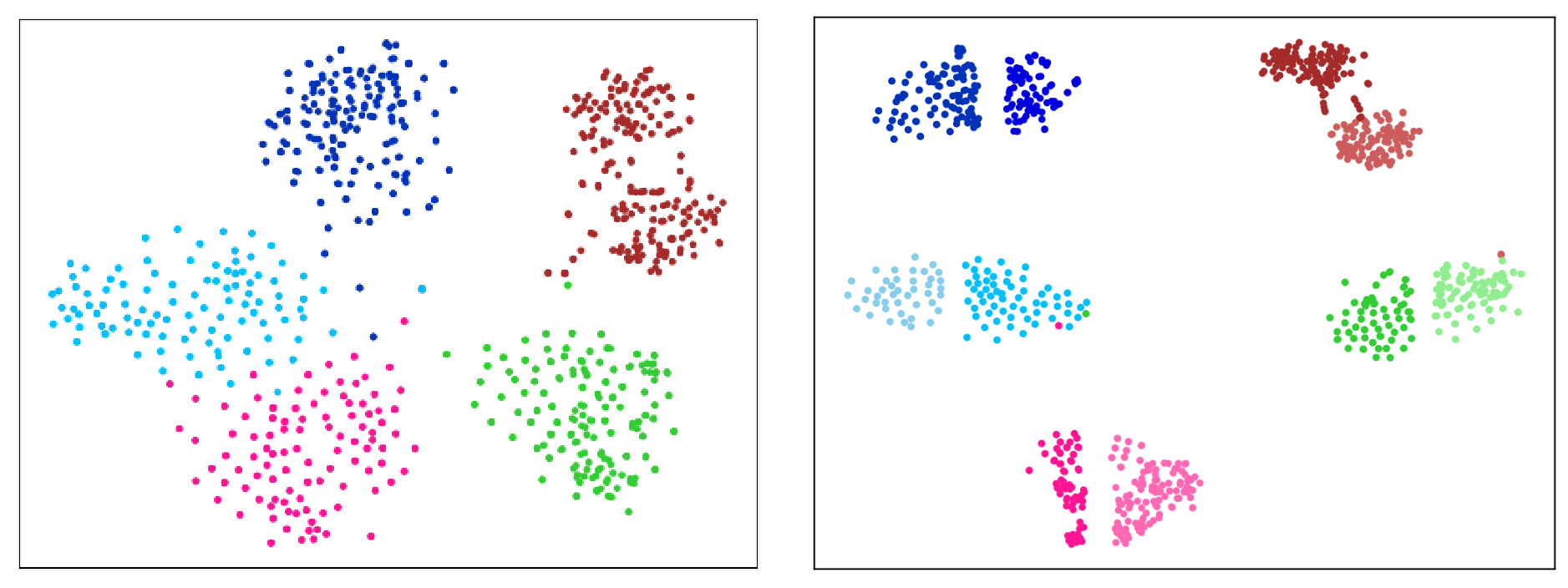
Figure 7. Embedding spaces learned by a parametric model (left), and the proposed nonparametric model (right). Only 5 classes and 2 prototypes per class are shown.

Additional results in the original paper include evaluation on more datasets, others examples of segmentations and ablation studies on the hyperparameters of the method.