Vision Transformer with Deformable Attention
Notes
- Code is available on github
Highlights
-
The succes of Transformers is attributed to the large receptive field. However it comes with a high computational cost.
-
Some approaches try to limit the attention mechanism such as Swin Transformer1 or Neighborhood Attention Transformer2, but they are data agnostic.
-
This article proposes a novel deformable self-attention module where the selection of tokens is learned.
-
The idea come from the deformables convolutions3 as Deformable DETR4, a concurent work.
-
In my opinion, the method is more a selective attention than a deformable attention.
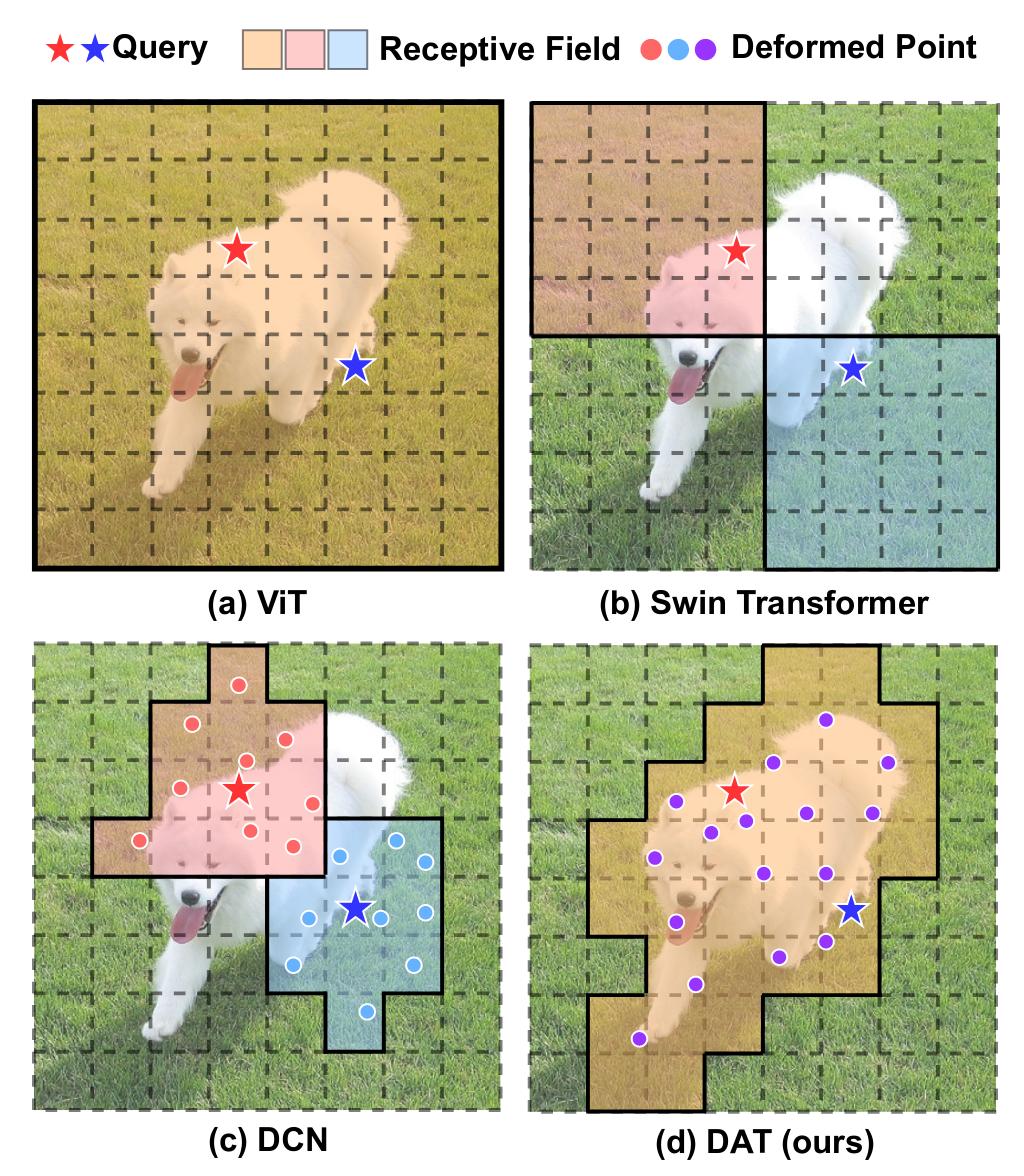
Figure 1 : Comparison of the receptive field with other visions Transformers and DCN.
Deformable Attention Transformer
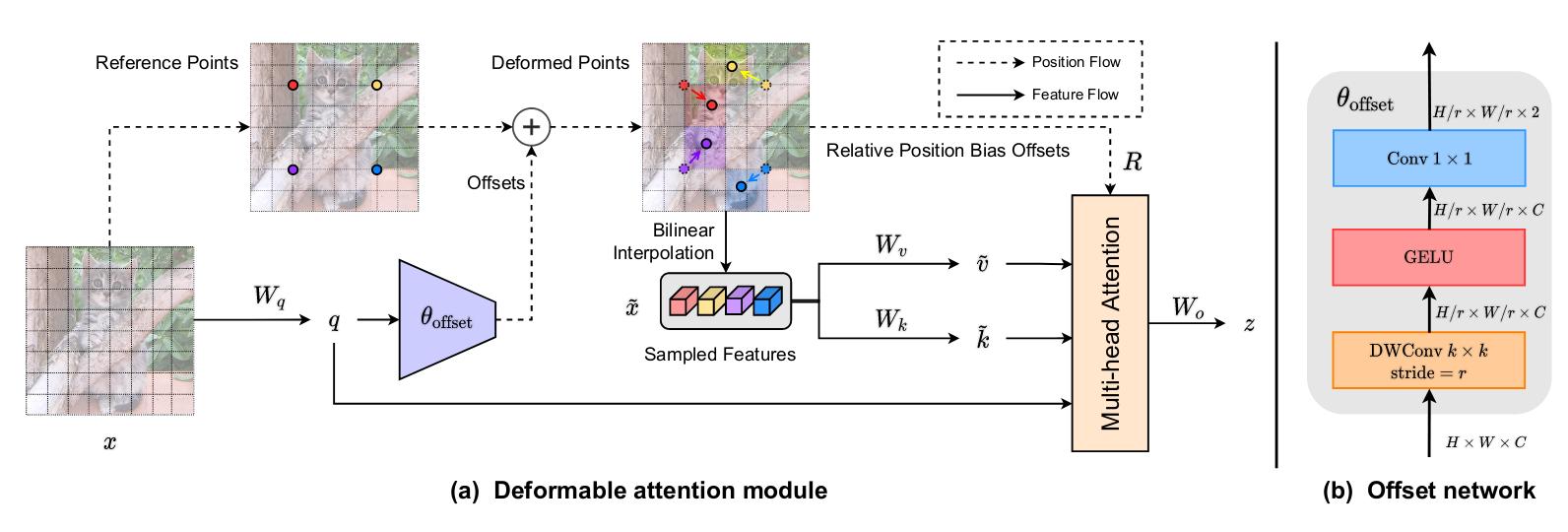
Figure 2 : Illustration of the deformable attention mechanism.
-
Standard multi-head self attention (MHSA) for \(M\) heads:
\[q = xW_q, \quad k = xW_k, \quad v = xW_v\] \[z^{(m)} = \sigma(q^{(m)}k^{(m)T}/\sqrt{d})v^{(m)}, \quad m=1,...,M\] \[z = Concat(z^{(1)},...,z^{(M)})W_o\]With normalization and residual connections:
\[z_{l}^{'} = MHSA(LN(z_{l-1})) + z_{l-1}\] \[z_{l} = MLP(LN(z_{l}^{'})) + z_{l}^{'}\] -
Deformable attention module
Given the input feature map \(x\in\mathbb{R}^{H \times W \times C}\) a uniform grid of points \(p \in \mathbb{R}^{H_G \times W_G \times 2}\) is generated.
More precisely, we downsample the feature map by a factor \(r\), \(H_G = H / r, W_G=W/r\).
The values of reference points are linearly spaced 2D coordinates \({(0, 0),...,(H_G -1,W_G-1)}\) then normalized to the range \([-1,1]\).
The query tokens matrix \(q\) is fed into the network \(\theta _{offset}(.)\) to generate the offsets \(\Delta p = \theta_{offset}(q)\).
The amplitude \(\Delta p\) is scaled by a factor \(s\), \(\Delta p = s \cdot tanh(\Delta p)\).
We have:
\[q=xW_q, \tilde{k}=\tilde{x}W_k, \tilde{v}=\tilde{x}W_v\] \[\tilde{x}=\phi(x;p+\Delta p)\]with \(\tilde{k}\) and \(\tilde{v}\) represent the deformed keys and values matrix and \(\phi(.;.)\) the sampling function set to:
\[\phi(z;(p_x,p_y))=\sum_{(r_x,r_y)}g(p_x,r_x)g(p_y,r_y)z[r_y,r_x,:]\]where \(g(a,b)=max(0,1- \vert a-b \vert )\).
Note that this sampling simply sums the four nearest neighbours of the sampled point
Finally, the output of one attention head is:
\[z_{(m)}=\sigma(q_{(m)}\tilde{k}_{(m)T}/\sqrt{d} + \phi(\hat{B};R))\tilde{v}_{(m)}\]where \(\phi(\hat{B};R)\in\mathbb{R}^{HW \times H_GW_G}\) is the relative positional embedding.
-
Offset generation
The network used for offset generation is composed of a \(5 \times 5\) depthwise convolution layer, a GELU activation and a \(1 \times 1\) convolution layer.
-
Offset groups
To promote the diversity of deformed points, the matrix \(q\) is split into \(G\) groups according to the channels. And each group is passed into the offset network to generate different offset that are then concatenated.
-
Deformable relative position bias
They adapt the standard relative positional encoding to deformable convolution to have the relative position between selected tokens. But this part is not really clearly explained.
-
Computational complexity
Similarly to the newest transformer architectures, the complexity is reduced (because we have less tokens) and the additional computational cost brought by the offset network is negligible (6% of the FLOPs for a module).
-
Model architecture

Figure 3 : DAT architecture.
A Transformer architecture is built upon this new attention mechanism.
The tokenization is performed by a \(4 \times 4\) non-overlapped convolution.
First two stages don’t use Deformable Attention.
Each stage is composed of a local attention block then a global attention block.
Experiments
- ImageNet-1K classification

DAT outperforms existing baselines by a small margin and is competitive with ConvNeXt5 (\(82.1\), \(83.1\), \(83.8\) and \(85.1\) respectively for model \(T, S, B\) and \(B\) with image size \(384 \times 384\))
- COCO Object Detection
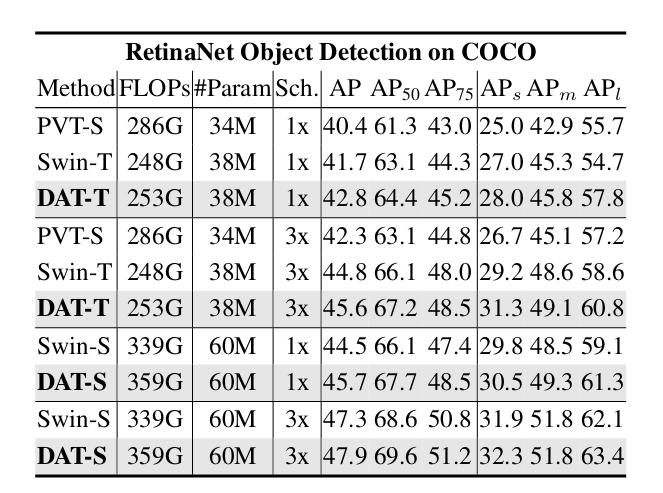
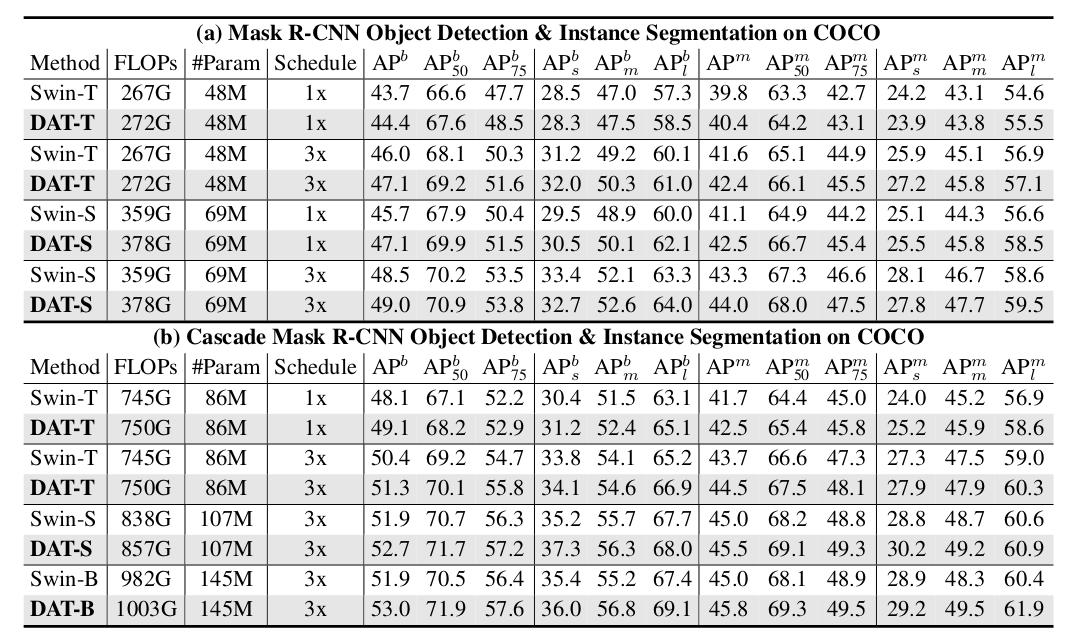
- ADE20K Semantic Segmentation
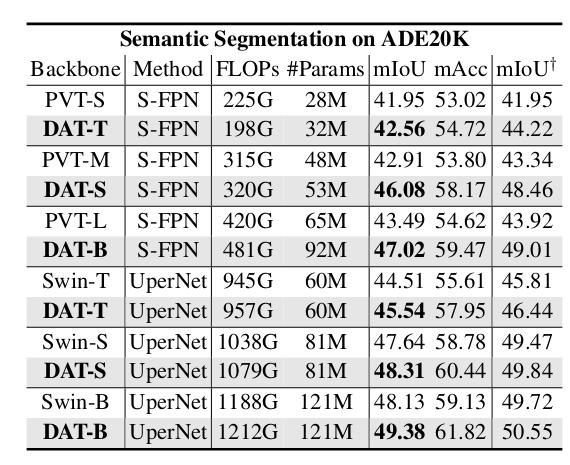
- Ablation Study
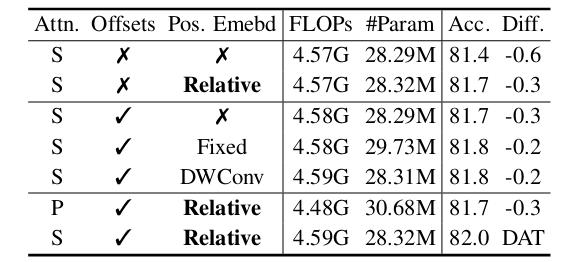
They test different positional embeddings and attention mechanism for the first two stages.

They test replacing the attention module by their Deformable Attention module in different stages.
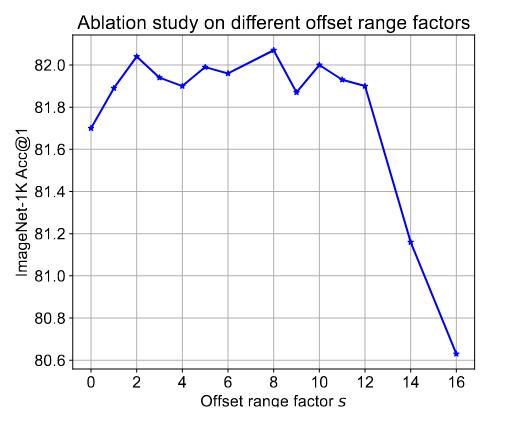
Figure 4 : Ablation study on different offset range factor s.
They test different range factors \(s\) showing that the model is pretty robust to this hyperpameter.
Note that given the size of the feature map in the third stage \(14 \times 14\) an offset superior to 14 is useless
-
Visualization

Figure 5 : Visualizations of the most important keys on COCO dataset.
Finally they give a visualization of the most important keys learned by the model for several images.
Conclusion
This article introduces a new deformable attention mechanism where a selection of usefull tokens is learned . It builds a transformer architecture based on this mechanism that achieves competitive results on different computer visions tasks.